IMS
Session Slot: 8:30-10:20 Monday
Estimated Audience Size:
AudioVisual Request:
Session Title: Stochastic Analysis
Theme Session: No
Applied Session: No
Session Organizer: Etheridge, Alison University of Oxford, UK
Address: Department of Statistics, 1 South Parks Road, Oxford, OX1 3TG, UK
Phone: +44 1865 272 860
Fax: +44 1865 272 595
Email: etheridge@stats.ox.ac.uk
Session Timing: 110 minutes total (Sorry about format):
Session Chair: Adler, Robert Technion
Address:
Phone:
Fax:
Email:
1. The Ancestral Selection Graph
Krone, Steve, University of Idaho
Address: Dept. of Mathematics, University of Idaho, Moscow, ID 83844
Phone: 208-885-6317
Fax: 208-885-5843
Email: krone@uidaho.edu
Abstract: Coalescent theory is currently one of the most active areas of population genetics. The idea is to study the genealogy of a (sample from a) population by viewing the history of a gene in the population backwards in time. In the neutral case (i.e., when there is no natural selection in the model), this approach has lead to a dramatic surge in our understanding of population genetics over the past 20 years. In this talk, we show how to use some simple ideas from interacting particle systems to construct genealogies for a large class of models involving selection and mutation. The genealogy of the sample is embedded in a graph which we call the ancestral selection graph. This graph contains all the information about the genealogy of the sample; it is the analogue of Kingman's coalescent process which arises in the case with no selection. The ancestral selection graph can be easily simulated and we outline an algorithm for simulating samples. The main goal is to analyze the ancestral selection graph and to compare it to Kingman's coalescent process. As applications, we will discuss things like the time to the most recent common ancestor of the sample and the probability of identity by descent. (This is joint work with Claudia Neuhauser.)
2. Stochastic Coalescent
Limic, Vlada, University of California at Berkeley
Address: Department of Statistics #3860 University of California, Berkeley Berkeley, CA 94720-3860
Phone: 510-642-2781
Fax: 510-642-7892
Email: vlada@stat.berkeley.edu
Abstract: The Marcus-Lushnikov(M-L) process was a very popular model of coagulation studied by theoretical physicists in the 1980's. A verbal description is: at time start with a configuration of n particles, each of mass 1, and let it evolve in continuous time according to the rule: each pair of clusters with masses x and y merges into a single cluster of mass x+y at rate K(x,y)/n. We give a motivation for the model and describe some typical questions in the field. There are many open problems.A generalization of the M-L process is the stochastic coalescent
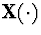, a vector-valued Markov process representing merging of possibly infinitely many clusters of mass. The transitions are induced by the dynamics: each pair of clusters with masses x and y merges into a cluster of mass x+y at rate K(x,y). If the rate kernel
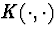is constant, this process is well-known Kingman's coalescent . Nice probabilistic representations exist also for the additive (K(x,y) = x+y) and the multiplicative (K(x,y) = xy) coalescent.
We introduce the entrance boundary problem, and present the solution for the multiplicative case, a joined work with David Aldous.
3. Genealogies of Spatially Structured Populations
Williams, David, Oxford University
Address: Department of Statistics,Oxford University 1 South Parks Road,Oxford OX1 3TG, England
Phone: +44-1865-2 72870
Fax: +44-1865-272595
Email: drew@stats.ox.ac.uk
Abstract: The coalescent process is used to identify useful biological quantities under very simple conditions. We incorporate a spatially dependent offspring law into the background population and compare the effects of such a modification relative to other, spatially structured, coalescent approaches.
List of speakers who are nonmembers: