


Next: asa.phys.es.04
Up: ASA Physical and Engineering
Previous: asa.phys.es.02
Sponsoring Section/Society: ASA-SPES
Session Slot: 10:30-12:20 Tuesday
Estimated Audience Size: 100-150
AudioVisual Request: Two Overheads
Session Title: Dimension Reduction
Theme Session: Yes
Applied Session: Yes
Session Organizer: Lin, Dennis K.J.
Penn State University
Address:
314 Beam Building, Penn State University,
University Park, PA 16802-1913
Phone: 814-865-0377
Fax: 814-863-2381
Email: DKL5@psu.edu
Session Timing: 110 minutes total (Sorry about format):
First Speaker - 25 minutes
Second Speaker - 25 minutes
Third Speaker - 25 minutes
Fourth Speaker - 25 minutes
Floor Discusion - 10 minutes
Session Chair: Li, Ker-Chau
UCLA
Address: Department of Mathematics, UCLA, LA. CA 90024
Phone: 310-8254897
Fax: 310-2066673
Email: kcli@math.ucla.edu
1. High Dimensional Data Analysis Via the SIR/PHD Approach
Li, Ker-Chau,
University of California, Los Angeles
Address:
Department of Mathematics, UCLA. LA. CA. 90024
Phone: 310-8254897
Fax: 310-2066673
Email: kcli@math.ucla.edu
Abstract:
Dimensionality is an issue that
can arise in every scientific field. Generally speaking,
the difficulty lies on how to visualize a high dimensional
function or data set. To investigate this issue, Li(1991, 1992)
proposed a dimension-reduction model of the form
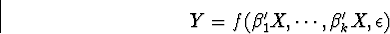
where X denotes the input and Y denotes the output variable.
This is general enough to
incorporate many regression models as special cases.
However, the novel feature about this model is that f is unknown
and so is the distribution of the random error 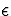 . The goal is
to find the
. The goal is
to find the 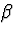 vectors so that they can be used to reduce the input
dimension when k is small.
Two simple methods, sliced inverse regression (SIR) and principal
Hessian directions (PHD) have been studied.
vectors so that they can be used to reduce the input
dimension when k is small.
Two simple methods, sliced inverse regression (SIR) and principal
Hessian directions (PHD) have been studied.
In this talk, I will give an overview on some recent results
about SIR/PHD and describe some ongoing research in various application
areas, including censored regression,
error-in-regressor, nonlinear confounding, functional data analysis,
nonlinear time series, Monte-Carlo and Bayesian computation, and others.
2. A Systematic Approach to the Analysis of Complex
Interaction Patterns in 2-Level Factorial Designs
Filliben, James J.,
National Institute of Standards and Technology
Address:
Statistical Engineering Division,
NIST North, room 353, Gaithersberg
MD 20899
Phone: 301-9752855
Fax: 301-9904127
Email: liu@cam.nist.gov
Li, Ker-Chau,
University of California, Los Angeles
Abstract:
Analysis of
data from two-level full factorial designs often ends up with
a final prediction equation which gives only the significant
main effect and interaction terms. When the number of
interactions is small, simple and useful interpretation of the equation
can then be drawn immediately.
This article addresses a different situation where the number of
significant interactions may be large so that additional efforts
are needed in order to sort out the pattern and the relationship
between them. In particular, we bring out a class of models where
most interactions can be attributed to just one or two (or a very small
number of) factors, and conditional on these factors,
the models become essentially linear.
We offer a strategy for uncovering this structure
by Linear Domain Splitting (LDS) whereby a
complicated global model is replaced by a series
of local domain-specific linear models. We
present a recommended methodology (PHD-principal
Hessian direction) for systematically
proceeding from the global equation to
local split-domain analyses. The net result is
that guided tree-structured paths are offered for
visiting the source-of-interaction factors
in sequence, which appropriately reflects their relative
importance and mutual relationship.
The final stage modeling is simpler (linear). The
quality of the fit can be assessed separately in each
region, and the analyst comes
away with greater insight as to the sensitivity
and robustness of the various factor effects over
various regions. Applications in digital electronics testing is
illustrated by analyzing a data set collected for studying the
conversion error of a digital-to-analog converter.
3. Uncertainty Analysis in Mathematical Modeling via
Statistical Dimension Reduction with Application in Groundwater Modeling
Horng, Ming-Jame,
Water Resources Bureau, MOEA, ROC
Address:
10F, 41-3, SEC. 3, Hsin-I Rd
Taipei, Taiwan, ROC
Phone: 02-7542080
Fax: 02-7542244
Email: mjhorng@wrb.gov.tw
Li, Ker-Chau,
University of California, Los Angeles
Yeh, William W-G,
Abstract:
Mathematical modeling is generally applied to describe various physical
systems in many scientific fields. A common way of understanding the
behavior of a mathematical model is through computer
simulation. Such a task often involves model parameters
which have to be set properly. Yet some model parameters
can be rather hard to determine. One such example
is a groundwater system used for predicting water head at
a designated well. The crucial model parameters
such as the hydraulic conductivity parameters in
various aquifer zones can at best be
estimated roughly from related geologic and hydrologic information.
The uncertainty from such input model parameters often
lead to substantial prediction error.
This article takes a new approach to uncertainty analysis of
mathematical models via a statistical dimension reduction method,
Sliced Inverse Regression(SIR). It generalizes
differential sensitivity analysis and is able to provide a global
view on the nonlinear relationship between the output and the
input model parameters.
4. A Three-Way Subclassification Approach to
Multiple-Class Discriminant Analysis
Chen, Chun-Houh,
Academia Sinica, ROC
Address:
Institute of Statistical Science, Academia Sinica
Taipei, Taiwan, ROC
Phone:
Fax: (886)-2-7831523
Email: cchen@stat.sinica.edu.tw
Li, Ker-Chau,
University of California, Los Angeles
Abstract:
Discriminant analysis problems are
much harder to handle when the number of classes k
is large. In view of
this tendency, a strategy based
on three-way subclassification is proposed. The original k-class
problem is first decomposed into k(k-1)/2 smaller problems,
each involving a 3-way classification between a pair of classes A
and B, and a combined third class which is just the union of
all other classes. Then the results from each
subcalssification will be synthesized under a conditional error
rate analysis. Our formulation of 3-way subclassification is ideal
for exploring the degree of unanimity among different decisions
made in subclassification. This advantage is illustrated well in
the context of hand-written digit recognition, using the data set
of LeCun et al(1989). A large portion of high quality images in the
test set can be easily filtered out by 3-way subclassification -
they are predicted with an error rate less than 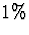 .
.
List
of speakers who are nonmembers: None



Next: asa.phys.es.04
Up: ASA Physical and Engineering
Previous: asa.phys.es.02
David Scott
6/1/1998
![]()