


Next: asa.stat.comp.03
Up: ASA Statistical Computing (5
Previous: asa.stat.comp.01
Sponsoring Section/Society: ASA-COMP
Session Slot: 8:30-10:20 Tuesday
Estimated Audience Size: 60-90
AudioVisual Request: None
Session Title: Bootstrapping Time Series
Theme Session: No
Applied Session: Yes
Session Organizer: Hesterberg, Tim
MathSoft/Statistical Sciences
Address: MathSoft/Statistical Sciences
1700 Westlake Ave. N, Suite 500
Seattle, WA 98109-3044
Phone: (206)283-8802x319
Fax: (206)283-0347
Email: timh@statsci.com
Session Timing: 110 minutes total (Sorry about format):
First Speaker - 35 minutes
Second Speaker - 35 minutes
Third Speaker - 35 minutes
Floor Discusion - 5 minutes
Session Chair: Hesterberg, Tim
MathSoft/Statistical Sciences
Address: MathSoft/Statistical Sciences
1700 Westlake Ave. N, Suite 500
Seattle, WA 98109-3044
Phone: (206)283-8802x319
Fax: (206)283-0347
Email: timh@statsci.com
1. Subsampling with unknown rates of convergence
Romano, Joseph P.,
Stanford University
Address: Department of Statistics
Stanford University
Stanford, CA 94305-4065
Phone: 650-723-6326
Fax: 415-725-8977
Email: romano@stat.Stanford.edu
Abstract:
I will give a brief overview of subsampling, as a general
method for the construction of large-sample confidence regions for a
general unknown parameter 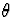 associated with the probability
distribution generating a stationary sequence
associated with the probability
distribution generating a stationary sequence 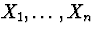 .In particular, subsampling can work when the bootstrap fails and the
general theory supports this statement. The subsampling methodology
hinges on approximating the large-sample distribution of a statistic
.In particular, subsampling can work when the bootstrap fails and the
general theory supports this statement. The subsampling methodology
hinges on approximating the large-sample distribution of a statistic
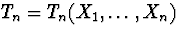 that is consistent for
that is consistent for 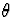 at
some known rate
at
some known rate 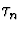 .
.
Although subsampling has been shown to yield confidence regions for
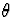 of asymptotically correct coverage under very weak
assumptions, the application of the methodology as it has been
presented so far is liminted if the rate of convergence
of asymptotically correct coverage under very weak
assumptions, the application of the methodology as it has been
presented so far is liminted if the rate of convergence 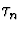 happens to be unknown or intractable in a particular setting. In
this talk, I will discuss how it is possible to circumvent this
limitation by (a) using the subsampling methodology to derivate a
consistent estimator of the rate
happens to be unknown or intractable in a particular setting. In
this talk, I will discuss how it is possible to circumvent this
limitation by (a) using the subsampling methodology to derivate a
consistent estimator of the rate 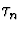 , and (b) employing the
estimated rate to construct asymptotically correct confidence
regions for
, and (b) employing the
estimated rate to construct asymptotically correct confidence
regions for 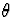 based on subsampling.
based on subsampling.
2. Matched-Block Bootstrap for Dependent Data
Kuensch, Hans-Ruedi,
Seminar fur Statistik, ETH Zurich
Address: Seminar fur Statistik
ETH Zentrum
CH-8092 Zurich
Switzerland
Phone: +41-1-632 3416
Fax: +41-1-632 1086
Email: kuensch@stat.math.ethz.ch
Abstract:
The block bootstrap for time series consists in randomly
resampling blocks of consecutive values of the given data and
aligning these blocks into a bootstrap sample. Hence in the
bootstrap sample, different blocks are independent whereas in the
original sample they are not. This impairs the performance of the
blockwise bootstrap, particularaly in cases where the dependence is
strong. Here we suggest a solution ot this problem by aligning with
higher likelihood those blocks which match at their ends. This is
achieved by resampling the blocks according to a Markov chain whose
transitions depend on the data. The matching algorithms we propose
take some of the dependence structure of the data into account.
They are based on a kernel estimate of the conditional lag one
distribution or on a fitted autoregression of small order.
Numerical and theoretical analyses in the case of estimating the
variance of the sample mean show that matching reduces bias and,
perhaps unexpectedly, has relatively little effect on variance. Our
theory extends to the case of smooth functions of a vector mean.
3. Estimation and Prediction for Time Series Using the
Bootstrap
Thombs, Lori,
University of South Carolina
Address: Department of Statistics
University of South Carolina
Columbia, SC 29208-0001
Phone:
Fax:
Email: thombs@math.sc.edu
Abstract:
We discuss two problems in time series analysis in which
the bootstrap proves to be a useful tool. It is a well known result
that if a process is pure white noise, then the autocorrelation
estimates, scaled by the square root of the sample size, are
asymptotically standard normal. We show that if the underlying
process is assumed to be uncorrelated rather than independent, the
asymptotic distribution is not necessarily standard normal. We
present general asymptotic theory for the estimated autocorrelation
function and discuss testing for lack of correlation without the
further assumption of independence. Appropriate resampling methods
are proposed which can be used to approximate the sampling
distribution of the autocorrelation estimates under weak
assumptions.
In a second application, the nonparametric bootstrap is applied to
the problem of prediction in autoregresion. Standard prediction
techniques for Gaussian time series utilize the result that the
conditional distribution of Y[t+k], given the data, is Gaussian as
well. As a nonparametric alternative, the bootstrap can be used to
estimate the conditional distribution of Y[t+k]. The bootstrap
replicated, being generated backward in time, all hav ethe same
conditionally fixed p-values at the end of the series. Simulations
are presented which illustrate the performance of the proposed
bootstrap prediction technique.
List
of speakers who are nonmembers: None



Next: asa.stat.comp.03
Up: ASA Statistical Computing (5
Previous: asa.stat.comp.01
David Scott
6/1/1998
![]() of asymptotically correct coverage under very weak
assumptions, the application of the methodology as it has been
presented so far is liminted if the rate of convergence
of asymptotically correct coverage under very weak
assumptions, the application of the methodology as it has been
presented so far is liminted if the rate of convergence ![]() happens to be unknown or intractable in a particular setting. In
this talk, I will discuss how it is possible to circumvent this
limitation by (a) using the subsampling methodology to derivate a
consistent estimator of the rate
happens to be unknown or intractable in a particular setting. In
this talk, I will discuss how it is possible to circumvent this
limitation by (a) using the subsampling methodology to derivate a
consistent estimator of the rate ![]() , and (b) employing the
estimated rate to construct asymptotically correct confidence
regions for
, and (b) employing the
estimated rate to construct asymptotically correct confidence
regions for ![]() based on subsampling.
based on subsampling.