Suppose (X,Y) are jointly distributed random variables and
we wish to ``predict'' Y from X. This situation arises
for instance when we will make an observation of X but not
of Y. As an example, X may be years of education and Y
may be annual income. It is typically easy to get data on X
and somewhat harder to get data on Y, so we may wish to predict
income from education. Our predictor of Y given X will of
course be some function of X, say 
.
We will measure the accuracy of prediction by so called
Mean Squared Prediction Error:
One can in fact find the best predictor (in the sense of minimizing MSPE) over all predictors, i.e.\ all functions of X, namely
where 
is the conditional density
However, it is sometimes desirable to restrict the class of predictors to so-called linear predictors, which are predictors of the form
where a and b are constants. It is easy enough to find the best linear predictor. For convenience, assume for now
We will show how to deal with nonzero means in a moment.
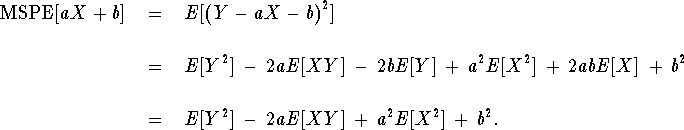
Taking (partial) derivatives and setting equal to 0 gives
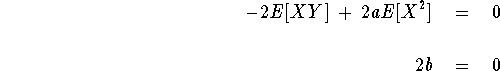
which gives
One can check that this indeed gives a minimum.
If (10) doesn't hold, then replace X by 
and similarly for Y. The previous result applies then to
and 
and says the best linear predictor
for given is
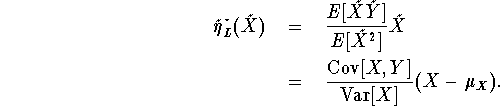
To get the best linear predictor of Y =
, we simply add 
:
Note that the corresponding optimal coefficients are
When one has data
, 
, 
, 
,
it is common to consider the linear function of x
which best predicts y in the data set. This
leads to the so-called least squares regression line,
which is defined by the slope a and intercept b
which minimize the Residual Sum of Squares
(abbreviated RSS)
It is easy enough to derive the least squares estimates of a and b:
Note the similarity with (12). In fact, the least squares line is perhaps best thought of as a sample based estimate of the best linear predictor. Thus, for example, if we wish to estimate the best linear predictor of income given education, we simply do least squares regression with a sample of (education, income) data.
