Santanu Chakraborty
University of Texas - Pan American

Zero Inflated Poisson and Zero Inflated Negative Binomial distributions are well known in the literature. They are used to model count data sets which have more zeros than usual Poisson or Negative Binomial datasets. So, the corresponding probability distributions have inflated masses at zero and deflated masses at nonzero points. But it should be appreciated that there are count data sets in the literature also with not only more zeros than a usual Poisson or Negative Binomial, but maybe more 1s, 2s and 3s. In that case, it makes more sense to inflate the original Poisson or Negative Binomial at 0, 1, 2 and 3. From this consideration, we introduce Finitely Inflated Poisson and Finitely Inflated Negative Binomial distributions into the literature. In this talk, we discuss Finitely Inflated Poisson (FIP) distribution. For example, an FIP with inflations at k points is defined as follows:



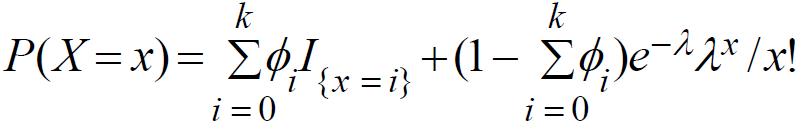
for x = 0, 1, 2, … where is the inflator at i for i = 0, 1, 2, _ _ _ , k. We talk about moments, moment generating function, convolutions of independent identically distributed FIP distributions and some parametric and Bayesian inferential issues for this distribution in this talk.