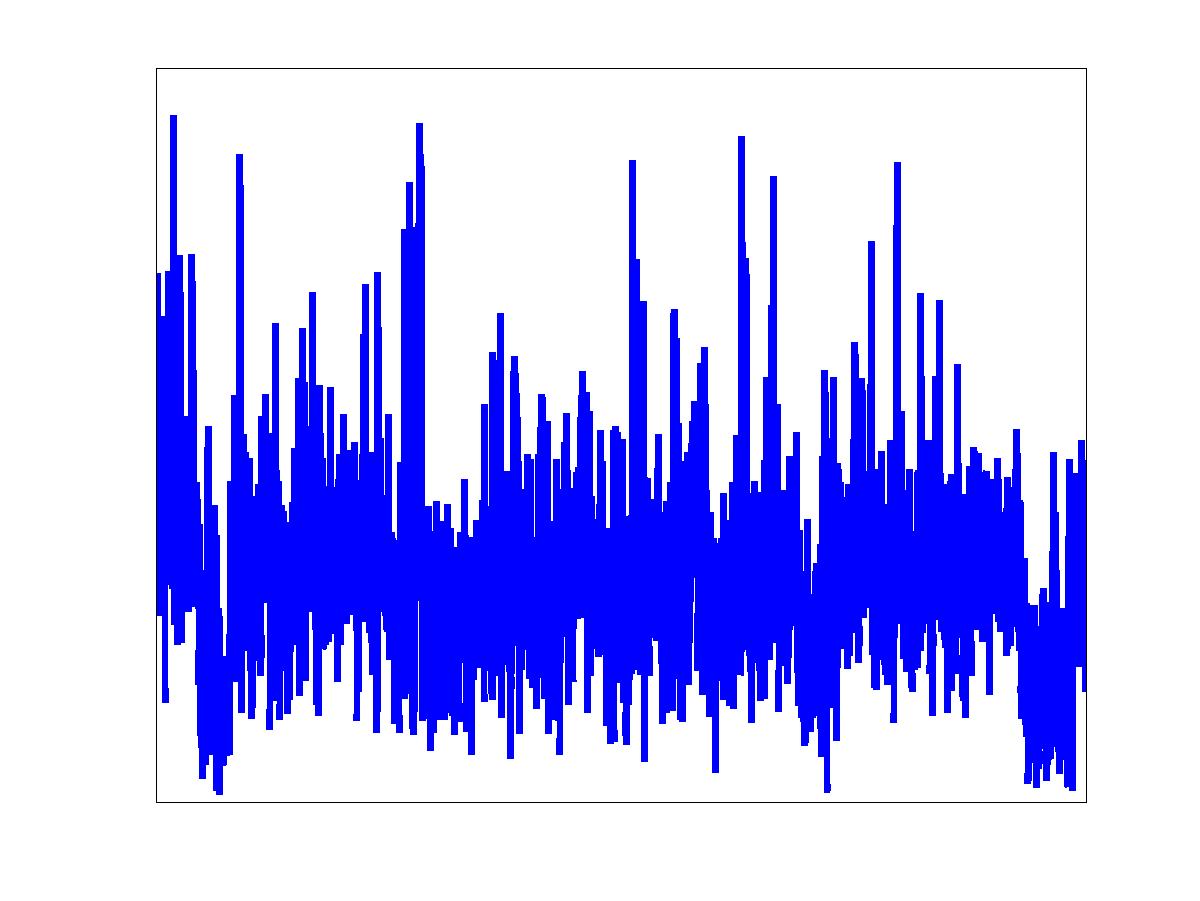

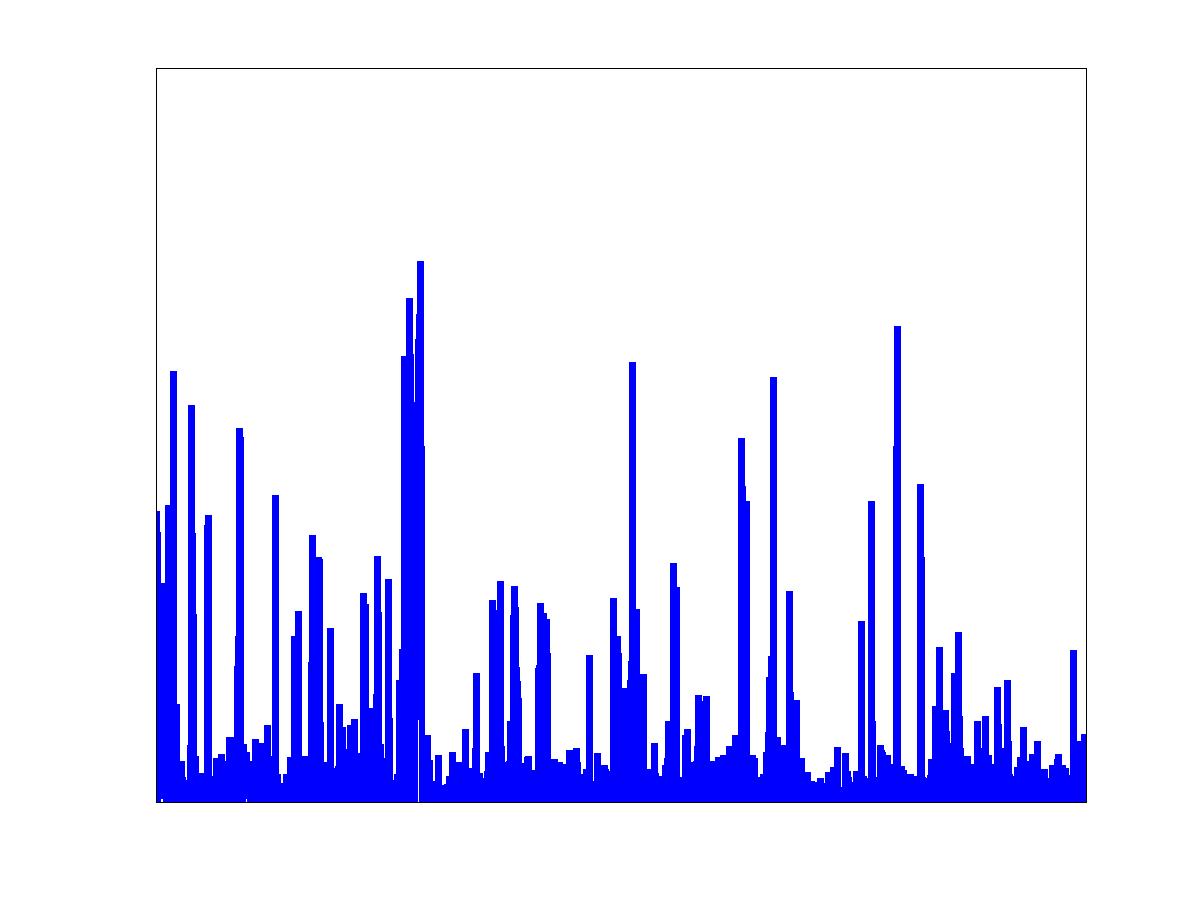

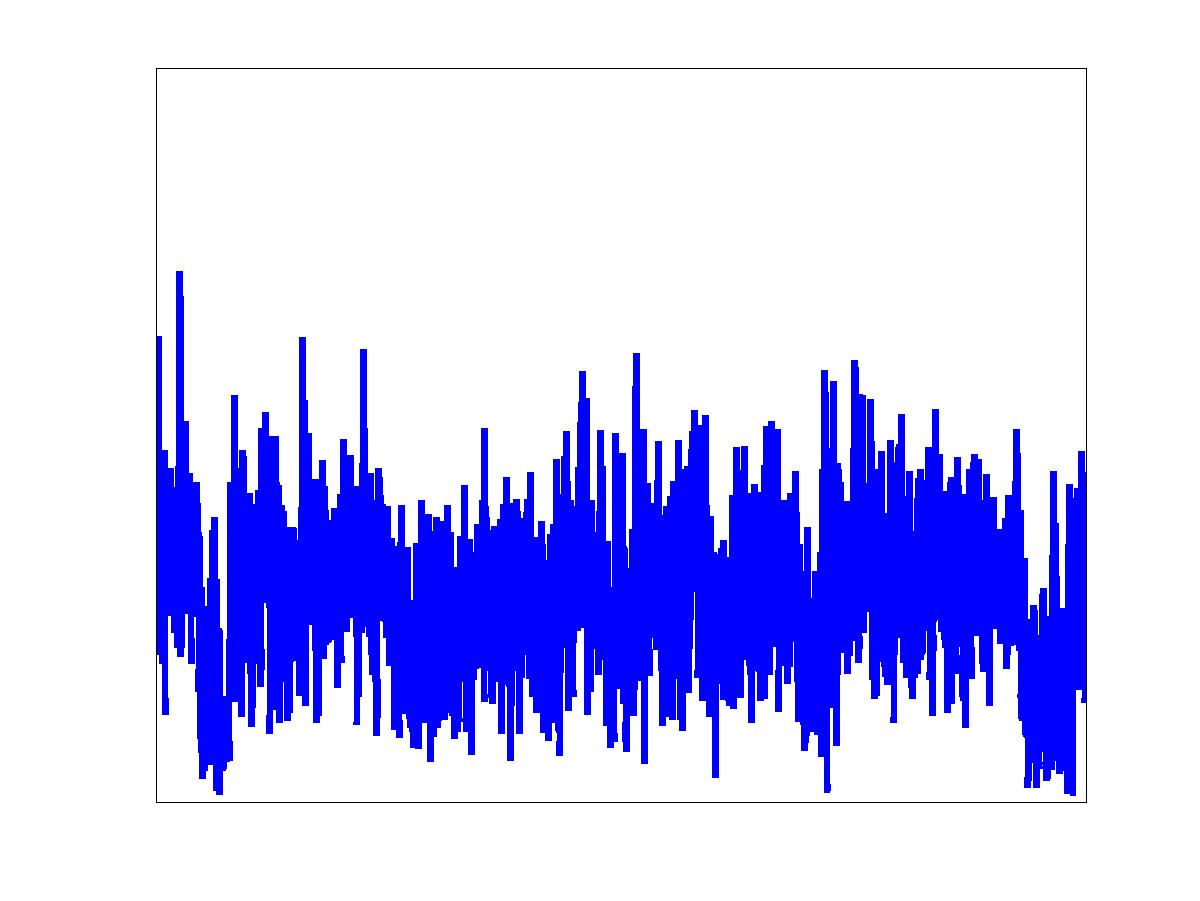
Alpha-beta modeling of network traffic
| Total traffic | Alpha traffic | Beta traffic | ||
|---|---|---|---|---|

|

|

|

|

|
| Aggregate network traffic exhibits fractal scaling behavior as well as non-Gaussianity (burstiness). | The non-Gaussianity -- or short time burstiness -- is caused by only a small fraction of all connections, called alpha connections. Alpha connections tend to have small round-trip times. | The remaining connections, called beta connections, contribute the bulk part of the data traffic, which is nearly Gaussian and non-bursty. The beta connections are responsible for the long-memory property which is typically present in network traffic. |
Most network traffic analysis and modeling studies lump all connections together into a single flow. Such aggregate traffic typically exhibits long-range-dependent (LRD) correlations and non-Gaussian marginal distributions. Importantly, in a typical aggregate traffic model, traffic bursts arise from many connections being active simultaneously. In this work, we present a new framework for analyzing and modeling network traffic that moves beyond aggregation by incorporating connection-level information. A careful study of many traffic traces acquired in different networking situations reveals (in opposition to the aggregate modeling ideal) that traffic bursts typically arise from just a few high-volume connections that dominate all others. We term such dominating connections Alpha traffic. Alpha traffic is caused by large file transmissions over high bandwidth links and is extremely bursty (non-Gaussian). Stripping the alpha traffic from an aggregate trace leaves a beta traffic residual that is Gaussian, LRD, and shares the same fractal scaling exponent as the aggregate traffic. Beta traffic is caused by both small and large file transmissions over low bandwidth links. In our alpha/beta traffic model, the heterogeneity of the network resources give rise to burstiness and heavy-tailed connection durations give rise to LRD. Queuing experiments suggest that the alpha component dictates the tail queue behavior for large queue sizes, whereas the beta component controls the tail queue behavior for small queue sizes.