

Next: About this document ...
Lab 1: A Brief Introduction to Systat, One-Sample Descriptive
Statistics, and the Normal Distribution
- [OBJECTIVES:] This lab is designed to familiarize the student with the
basic workings of Systat along with some
basic descriptive statistics, for one-sample data in particular.
Both summary statistics and graphics will be explored. Although
the methods in this lab are applied to one-sample data, most can be
used with other types of data and problems. Also, some basic
properties of Normal distributions, in particular scaling and shifting,
will be introduced.
- [DATA:] Usually this section is used to describe the data used in the
lab. Today, the data will be described later on in the lab where it is more
useful to do so.
- [DIRECTIONS:] Read the instructions that follow and
write out your answers to the questions
neatly and turn them in to the lab instructor.
- 1.
- GETTING STARTED. On your screen there should be an icon that reads
``Computer's Hostname''. This will be different for each machine. Double
click on it. This should open up a window containing several folders, one of
which reads ``Systat 5.2.1''. Double click on that one. Next double click
on the ``Systat.5.2.1§'' icon. At this point you should be in SYSTAT.
- 2.
- SYSTAT DATA FILES. Much of the data we will work with is already in
SYSTAT. To open one of these
files, go to the File menu and select Open.... A window will
appear. One of the possible files to choose will be a folder
entitled Data Files (to get here it might be necessary to click on
``Desktop'' and then ``Name of Your Computer'' and then on the ``Systat''
Folder). Select this folder by double clicking
on the folder. You can now open one of the data
files by double clicking on the name of the file. At this time, we
would like to open the file MEDICAL. When you do this,
the data editor should appear. The data editor is a spreadsheet
containing the variables and cases corresponding to the data file
you have selected. If the data editor does not appear, pull down
on the Window menu. Select the option Editor by pulling
down on the menu and releasing the mouse when you get to the
option Editor. The data editor should pop up automatically.
- 3.
- This file (MEDICAL) contains information obtained from the results of the 1986
census. The data represent the mortality rates in each state for
various causes of death. The first five columns give information about
state, region, and division of the census.
We will not be using these.
The next seven columns
contain the variables that correspond to the death rates. The title
of the column represents the type of death.
- 4.
- Choose one of the variables
on death rates (ACCIDENT, CARDIO, CANCER, PULMONAR, PNEU_FLU, DIABETES, or LIVER) and do the following.
- 5.
- ANALYSIS. Typically, we will begin labs by examining the basic
descriptive statistics of the data. This will include such things as
sample means, standard deviations, and other numerical summaries.
To calculate these descriptive statistics, go to the the Stats
option of the Stats menu and select Statistics....
A window will appear
with the column names of our data. Highlight whichever data set you
chose and hit select. In the lower right corner, you will see the
options for statistics to calculate. Some of the statistics may seem
foreign. We will be discussing these more in class and in lab.
- 6.
- Calculate and record the basic summary statistics, including the
mean, variance,
standard deviation, and skewness. To do this, simply select the
stats desired and hit OK, after you select your variable of choice.
Remember the mean and the standard deviation
are good measures of central tendency, the mean measuring location
and the standard deviation measuring dispersion.
What is the formula for variance in terms of standard deviation?
- 7.
- We will also be looking at various graphical representations of this
data.
- 8.
- Look at a histogram of the data, by selecting histogram under
the Density option of the Graph menu. Once there, select
your variable of choice by highlighting it and hitting Select.
This should put your variable name in the box between Select
and OK. Now hit OK and the graph should appear in the
Systat View window.
- Is the data symmetric or is it skewed?
- An outlier can be defined as a data point that lies quite far
from the bulk of the data. Such points can be caused by
recording errors, equipment malfunctions, etc. Outliers may also
be genuine data points which tell us something important and
unexpected about the data. These points must
be identified and examined to determine their cause and their
effect on subsequent calculations. Outliers can be identified
through descriptive statistics. Are there any points that you
might label as outliers in you data based upon the histogram?
- From the graph, what is the approximate center of the data? How
does this compare with the mean you calculated earlier?
- 9.
- Look at a stem and leaf plot. Select Stem under the Graph
menu.
- How is this plot different from the
histogram? How is it the same?
- Two of the advantages of this type
of representation are that it shows each data point and that they
are sorted. What additional information does it give you?
- The stem and leaf plot gives you two more measures of central tendency,
the median (location) and the interquartile range (dispersion).
Do the median and the interquartile range give a better representation
of the center and spread than the mean and standard deviation?
How does the symmetry or skewness of the data affect your answer?
- 10.
- Look at a boxplot. Select Box under the Graph menu.
The boxplot also uses the median and the interquartile range.
- What information does the boxplot give you that the other
graphical methods do not?
- What are the advantages and disadvantages to using a boxplot?
- 11.
- Summarize your results, including any observations or comments on
choosing the mean or median as a measure of location and how
the skewness of the data affects that choice. Also include your
opinions on which types of graphical representation are better
suited to displaying the shape of the data and showing outliers.
- 12.
- ENTERING DATA I. We will also be working with data that is not
already supplied in SYSTAT. To enter data into SYSTAT, go
to the File menu and select New. An empty SYSTAT Data Editor
will appear (provided that the Editor option under the
Window menu is active). Title 4 columns
NORM1, NORM2, NORM3, and NORM4.
Use the Fill Worksheet option under the Data menu
to fill the worksheet to 200 rows. Then, use the Math option under the Data menu to
set NORM1 to ZRN (select NORM1 on the left, ZRN on the
right). This fills the column with a sample of 200 values taken
at random from a standard Normal distribution.
Repeat this procedure for NORM2 through NORM4.
The population mean and variance of a standard normal
(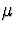 and
and 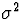 ) are and 1, repectively.
) are and 1, repectively.
- What are the sample means and sample variances of NORM1, NORM2,
NORM3, and NORM4? Are the sample means close to the
true mean of ? Are the sample variances close to the
true variance of 1?
- Using Graph/Density/Histogram, plot NORM1. Do the values
appear to be normally distributed (ie, does the
histogram appear bell shaped, subject to sampling error)?
- Using Data/Math, set NORM1 to NORM1*4 + 10.
This is equivalent to scaling the data so that the
population standard deviation
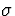 is now 4 and the the
population mean
is now 4 and the the
population mean 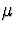 is now 10. How well do the sample
mean and standard deviation match these values?
is now 10. How well do the sample
mean and standard deviation match these values?
- Using Graph/Density/Histogram, plot NORM1. How does this
plot differ from that in part (b)? Keep this plot around for
the next few questions.
- If we draw numbers repeatedly from a standard normal,
then the relative frequency with which we observe values
less than 1.645 is about 0.95.
Let X be the value drawn from the standard normal.
Let Y=4*X + 10, a number drawn from a scaled and shifted normal.
Let k1 = 4*1.645 + 10 = 16.58. Do not worry about how we arrived at
these numbers right now.
Then the relative frequency with which the Y values will be
less than k1 should be about 0.95.
From the plot in (d), does this look beliveable?
- As the standard normal is symmetric about zero, the relative
frequency with which we observe values greater than -1.645
will be the same as the relative frequency with which we observe
values less than 1.645, namely about 0.95. Similarly the
relative frequency with which we observe values less than -1.645
will be about 1 - 0.95 = 0.05. Again,
let X be the value drawn from the standard normal, and
let Y=4*X + 10, a number drawn from a scaled and shifted normal.
Let k2 = 4*-1.645 + 10 = 3.42. Again, the important concept is not
how we arrived at the value of k2. The relative frequency with
which the Y values exceed k2 should be about 0.95.
From the plot in (d), does this look beliveable?
- Let us say that we want to know the relative frequency
with which a value drawn from a
normal distribution with mean 10 and standard deviation 4
takes on a value between 3.42 and 16.58.
What relative frequency would we expect?
From the plot in (d), does this
look believable?


Next: About this document ...
Dennis Cox
1/23/1998
![]() and
and ![]() ) are and 1, repectively.
) are and 1, repectively.
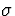 is now 4 and the the
population mean
is now 4 and the the
population mean 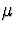 is now 10. How well do the sample
mean and standard deviation match these values?
is now 10. How well do the sample
mean and standard deviation match these values?