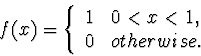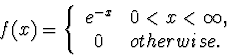Lab 4: The Central Limit Theorem and Binomial RVs

• [OBJECTIVES:] The central limit theorem will be demonstrated using several different types of random variables. We will begin with uniform random variables. Uniform random variables are continuous random variables which are equally likely to take on any value in the range [0,1]. The probability density function for a uniform random variable looks like a boxcar:

  $$f(x) = \left\{ \begin{array} {cl} 1 & 0<x<1, \\ 0 & otherwise. \end{array} \right.$$

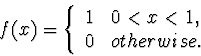
  When we roll a 6-sided die, we're equally likely to get any integer value in the range 1-6. If we think of increasing the number of sides on the die, and dividing the number shown by the total number of sides, the numbers that result are well approximated by a uniform distribution (ie, they are mimicked by uniform random variables).

  We then deal with exponential random variables. Exponential random variables are continuous random variables which are more likely to have values close to zero than far away from it. The probability function shows a very rapid decay:

  $$f(x) = \left\{ \begin{array} {cl} e^{-x} & 0<x<\infty, \\ 0 & otherwise. \end{array} \right.$$

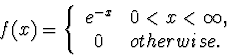
  Typical examples of exponential random variables include waiting times until the first occurrence of an event.

  Uniform random numbers fall evenly on either side of the mean of the distribution (0.5). Consequently, this distribution is said to be ``symmetric''. The Exponential random numbers, on the other hand, are ``lumped up'' on one side. This distribution is said to be ``skew'' (for lopsided). This will turn out to matter below.

• [DATA:] The data for this lab will be simulated (constructed) by Systat.
• [DIRECTIONS:] Be sure to answer all questions. Write out all answers to the questions neatly and turn them in to the lab instructors.

1.

Open up a new data file in Systat. Title 6 columns UNIF1, UNIF2, UNIF3, UNIF4, UNIF5 and UNIFSUM. Use the Fill Worksheet option under the Data menu to fill the worksheet to 200 rows. Then, use the Math option under the Data menu to set UNIF1 to URN (select UNIF1 on the left, URN on the right). Repeat this procedure for UNIF2 through UNIF5. The population mean and variance of a uniform random variable ($\mu$ and $\sigma^2$) are $\frac{1}{2}$ and $\frac{1}{12}$, repectively.

• What are the sample means and variances of UNIF1, UNIF2, UNIF3, UNIF4, and UNIF5 (give at least 3 decimal places)? Remember that by not selecting any variables, Systat will calculate the mean and variance of each variable. If your computer is giving you less than 3 decimal places, you can change this by going to Edit and then selecting Preferences. You should change the number of decimal places in the Analysis area as well as in the Editor area. Are the sample means close to the expected value of $\frac{1}{2}$? Are the sample variances close to the theoretical value of $\frac{1}{12}$?
• Using Graph/Density/Histogram, plot UNIF1. Do the values appear to be uniformly distributed (ie, does the histogram appear boxcar shaped, subject to sampling error)?

2.

The Central Limit Theorem says that if we add several random variables with the same pmf or pdf together, the shape of the pmf or pdf for the sum begins to tend towards a bell shape (a Normal random variable). Using Data/Math, set UNIFSUM equal to UNIF1+UNIF2+UNIF3+UNIF4+UNIF5.

• Use Graph/Density/Histogram to plot UNIFSUM. Has the boxcar shape largely disappeared? The Histogram function has a ``Smooth'' option. Choose the Normal suboption under Smooth. This will overlay a Normal curve on the histogram. Does the Normal curve appear to fit the histogram well?
• The entries in UNIF1 through UNIF5 are all independent random variables. As a result, the population means and variances add. Thus, for UNIFSUM, the mean should be $\frac{5}{2}$ and the variance $\frac{5}{12}$. Do the sample values seem to match the theoretical ones?
• We would expect approximately 68% of the values to fall within one standard deviation of the mean for a Normal random variable. Sketch the ``approximating'' Normal curve which Systat drew over the histogram of UNIFSUM. Be sure to label the UNIFSUM axis on your paper. Using your values for the sample mean and variance, calculate $sample \ mean \pm \sqrt{sample\ variance}$. Label this interval on your sketch. Does it seem plausible that 68% of the UNIFSUM values fall in this interval?

3.

Add 6 more columns and title them EXP1 throug EXP5 and EXPSUM. Using Data/Math, set EXP1 equal to ERN (``exponential random number'') and repeat for EXP2 through EXP5. The population mean and variance of an exponential random variable ($\mu$ and $\sigma^2$) are both 1.

• What are the sample means and variances of EXP1, EXP2, EXP3, EXP4, and EXP5? Are the sample means close to the expected value of 1? Are the sample variances close to the theoretical value of 1?
• Using Graph/Density/Histogram (remove the Smooth/Normal option by clicking on the black square) plot EXP1. Does the shape of the pdf show through clearly? Choose the Window/Graph Placement/Append Graph option. Plot a histogram of EXP2. Compare this with the plot of EXP1. Are you willing to believe that the differences are due to sampling error?

4.

The Central Limit Theorem does not work as well for skewed random variables as it does for symmetric ones. Hopefully this will show up now. Using Data/Math, set EXPSUM equal to EXP1+EXP2+EXP3+EXP4+EXP5.

• Use Graph/Density/Histogram to plot EXPSUM. Has the decay shape largely disappeared? Choose Smooth/Normal. Does the Normal curve appear to fit the histogram well? As well as it did for UNIFSUM?
• The entries in EXP1 through EXP5 are all independent random variables. As a result, the population means and variances add. Thus, for EXPSUM, the mean should be 5 and the variance 5. Do the sample values seem to match the theoretical ones?
• We would expect approximately 68% of the values to fall within one standard deviation of the mean for a Normal random variable. Using your values for the sample mean and variance, calculate $sample \ mean \pm \sqrt{sample\ variance}$. Do 68% of EXPSUM values roughly fall within this interval?

5.

Simulated data are commonly used to test out statistical techniques. Since we know the true pmf or pdf, we can predict what results we should get, and if we don't get them we know that something needs to be fixed. If the uniform random number generator is working correctly, we would expect roughly 80% of the values in UNIF1 to be above 0.2. In testing this, we can turn the numbers in UNIF1 to the outcomes from a binomial random variable with n=1 and p=0.8. Go under Data/Recode, and if UNIF1 > 0.2, let UNIF1 =1 (a success). Then, if UNIF1 < 0.2, let UNIF1 =0 (a failure). The mean of this random variable should be p=0.8 and the variance should be p(1-p) = 0.16. How well do the sample values match the theoretical ones?