- 1.
- Open up a new data file in Systat. Title 7 columns
NORM1, NORM2, NORM3, NORM4, NORMAVG, LOWBND and UPBND.
Use the Fill Worksheet option under the Data menu
to fill the worksheet to 200 rows.
Then, use the Math option under the Data menu to
set NORM1 to ZRN (select NORM1 on the left, ZRN on the
right). This fills the column with 200 values taken
at random from a standard Normal distribution.
Repeat this procedure for NORM2 through NORM4.
The population mean and variance of a standard normal
(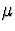 and
and 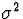 ) are and 1, repectively.
) are and 1, repectively.
- 2.
- Using Data/Math,
set NORMAVG to (NORM1 + NORM2 + NORM3 + NORM4)/4.
You will see
in class that the probability that a standard normal
random variable Z is between -1.645 and 1.645
is 0.90. You will also see (or may already have seen) that
if
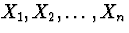 are n are iid
are n are iid 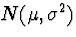 random variables then
random variables then 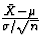 will
be N(0,1). Thus,
will
be N(0,1). Thus,
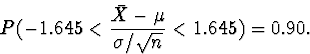
Let's rearrange this. Multiply all terms in the inequality
by 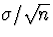 , subtract
, subtract 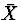 from all terms, and multiply all terms
by -1. This gives
from all terms, and multiply all terms
by -1. This gives
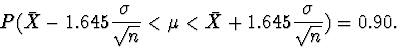
Thus, for each sample we can construct an interval
which we are ``90% confident'' contains the true
mean 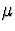 .
Here, we know that
.
Here, we know that 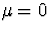 and
and 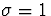 . Thus,
. Thus,
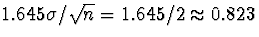 . Using Data/Math, set LOWBND to NORMAVG - 0.823,
and UPBND to NORMAVG + 0.823. We expect the
true population mean, , to lie in about
. Using Data/Math, set LOWBND to NORMAVG - 0.823,
and UPBND to NORMAVG + 0.823. We expect the
true population mean, , to lie in about 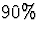 of the (LOWBND,UPBND) intervals. As we filled the
data tables to 200 rows, this means that we expect
about 20 cases where we don't catch the true mean.
of the (LOWBND,UPBND) intervals. As we filled the
data tables to 200 rows, this means that we expect
about 20 cases where we don't catch the true mean.
The reason we call this a ``confidence interval'' and not a
probability interval is that the true mean has a specific value.
For a given sample, the probability that the true mean is
in the confidence interval associated with that sample is either
0 or 1. What we know is that if we construct intervals in this
way for a lot of samples, we will catch the true mean some specified
fraction of the time.
- 3.
- Now, before we used a value of 1 for the standard deviation, this
being the true population value. What if we didn't know this value?
Then we would have to substitute an estimate of
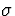 . The
most obvious estimate is the sample standard deviation s. Create
a new column, STDEV. Using Data/Math, set STDEV to
STD(NORM1,NORM2,NORM3,NORM4). Then, set UPBND to NORMAVG
+ 0.98*STDEV, and LOWBND to NORMAVG-0.98*STDEV.
. The
most obvious estimate is the sample standard deviation s. Create
a new column, STDEV. Using Data/Math, set STDEV to
STD(NORM1,NORM2,NORM3,NORM4). Then, set UPBND to NORMAVG
+ 0.98*STDEV, and LOWBND to NORMAVG-0.98*STDEV.
How many of these confidence intervals contain the true mean?
Is this consistent with 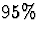 confidence? Do the intervals need to
be made wider (to catch more often) or shorter?
confidence? Do the intervals need to
be made wider (to catch more often) or shorter?
- 4.
- We now want to take our intuitions from simulating confidence
intervals to a real data set. The Cavendish data is as follows:
| 5.50 |
5.55 |
5.57 |
5.34 |
5.42 |
5.30 |
| 5.61 |
5.36 |
5.53 |
5.79 |
5.47 |
5.75 |
| 4.88 |
5.29 |
5.62 |
5.10 |
5.63 |
5.68 |
| 5.07 |
5.58 |
5.29 |
5.27 |
5.34 |
5.85 |
| 5.26 |
5.65 |
5.44 |
5.39 |
5.46 |
|
- 5.
- Open a new data file, title a column CAVEND and enter the above data
in that column.
- 6.
- The best modern measurements of the density of the earth correspond to a
measurement of 5.517 in Cavendish's experiment. One way to evaluate
Cavendish's results is to use them to come up with a range of
values for the true density of the earth which are plausible
at some degree of confidence - in short, to construct a confidence
interval for the the true value of the earth's density. We will
say that any value within this interval is plausible given this
data. The problem now is to choose how wide to make this interval.
If we make it too wide, the interval will contain the true value,
but it will not let us make precise statements about it. If it is
too short, we can make precise statements, but our statements
are likely to be wrong. Thus, we must compromise. We will try to
construct an interval that is as short as possible subject to
the constraint that the probability of our making a mistake is
quite small. We need to set a probability of excluding the true
value which we are willing to live with. This probability of
saying that the true value is not plausible is said to be the
level of significance associated with our test and is
denoted
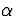 . The most common values chosen for
. The most common values chosen for 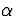 in practical work are .10 and .05, corresponding to making
a mistake one time in 10 or making a mistake one time in 20.
In this case, we will let
in practical work are .10 and .05, corresponding to making
a mistake one time in 10 or making a mistake one time in 20.
In this case, we will let 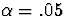 . Thus, we want to
choose the upper and lower bounds on our interval
in such a way that
. Thus, we want to
choose the upper and lower bounds on our interval
in such a way that
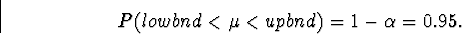
This probability is difficult to evaluate. So, we look for an
interval involving 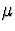 whose probabilities we can evaluate.
By the Central Limit Theorem, the sample mean is normally
distributed about the true mean of the population,
whose probabilities we can evaluate.
By the Central Limit Theorem, the sample mean is normally
distributed about the true mean of the population,

Now, if we knew the
true standard deviation 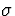 associated with these measurements,
we could compute an interval of the following form
associated with these measurements,
we could compute an interval of the following form
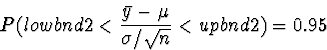
using the fact that the quantity in the middle has a standard
Normal distribution. It turns out that the shortest intervals
that we can construct are those which divide the probability
of making a mistake evenly between values which are too large
and those which are too small. In other words, half of the time
we make a mistake it will be by saying the true value is too
large to be plausible, and the other half it will be by saying
the true value is too small to be plausible. In the context of
the standard Normal shown above, this corresponds to choosing
a value for upbnd2 such that a standard Normal will exceed that
value only .025 of the time and a value of lowbnd2 such that
a standard Normal will be less than that value only .025 of the
time. These values are 1.96 and -1.96, respectively.
Since we do not know 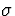 , we use the sample standard
deviation s in its place. This means that we have to replace
the normal values with those from a Student t distribution
with n-1 degrees of freedom. (You will learn about this procedure in
a couple of weeks in class; for now, just accept that it is valid.)
For a t-distribution with
28 degrees of freedom, the upper and lower bound values can
be found from Table E of your book to be 2.048 and -2.048.
Thus,
, we use the sample standard
deviation s in its place. This means that we have to replace
the normal values with those from a Student t distribution
with n-1 degrees of freedom. (You will learn about this procedure in
a couple of weeks in class; for now, just accept that it is valid.)
For a t-distribution with
28 degrees of freedom, the upper and lower bound values can
be found from Table E of your book to be 2.048 and -2.048.
Thus,
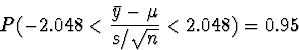
and
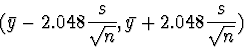
is a 95% confidence interval for the true mean.
- Is the true value of 5.517 in this interval? In order to figure
this out, you will need to find the sample mean
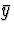 and standard
deviation s. To do this (just in case you have forgotten how), go to stats/stats/statistics.
and standard
deviation s. To do this (just in case you have forgotten how), go to stats/stats/statistics.
- Are Cavendish's measurements and the modern value
of the density of the earth significantly different? Give possible
explanations for a discrepancy, if one exists. If you were presenting
your results to modern scientists, what would you tell them about
Cavendish's experiment?
- If we were willing to tolerate a higher probability of
error (such as
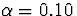 ) could we make more or less
precise statements about the plausible values? Is a 90%
confidence interval longer or shorter than a 95% interval?
) could we make more or less
precise statements about the plausible values? Is a 90%
confidence interval longer or shorter than a 95% interval?
![]() and
and ![]() ) are and 1, repectively.
) are and 1, repectively.
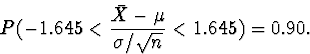
![]()
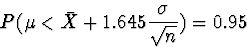
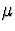 being less than UPBND.
How well does the observed value match the predicted
value?
being less than UPBND.
How well does the observed value match the predicted
value?
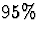 confidence
interval (check the tables). Reset LOWBND to NORMAVG - 0.98
and UPBND similarly. In how many cases is the true mean
not in the confidence interval? How well does this
match the theoretical prediction? Note that we are now ``
confidence
interval (check the tables). Reset LOWBND to NORMAVG - 0.98
and UPBND similarly. In how many cases is the true mean
not in the confidence interval? How well does this
match the theoretical prediction? Note that we are now ``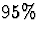 confident'' that our new interval contains the true mean, so the
predicted value here is 0.05 * 200 = 10. Also note that to achieve
higher confidence, we had to make our intervals wider.
confident'' that our new interval contains the true mean, so the
predicted value here is 0.05 * 200 = 10. Also note that to achieve
higher confidence, we had to make our intervals wider.
![]() confidence? Do the intervals need to
be made wider (to catch more often) or shorter?
confidence? Do the intervals need to
be made wider (to catch more often) or shorter?
![]()
![]()
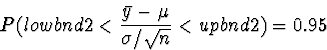
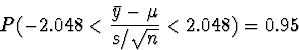
![]()
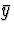 and standard
deviation s. To do this (just in case you have forgotten how), go to stats/stats/statistics.
and standard
deviation s. To do this (just in case you have forgotten how), go to stats/stats/statistics.
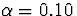 ) could we make more or less
precise statements about the plausible values? Is a 90%
confidence interval longer or shorter than a 95% interval?
) could we make more or less
precise statements about the plausible values? Is a 90%
confidence interval longer or shorter than a 95% interval?