(i) deciding whether or not two methods for determining the atomic weight of carbon differ, and
(ii) deciding whether or not babies of mothers who smoke have lower birth weights than babies of mothers who do not smoke.
![]()
![]()
and that ![]() are mutually independent. We
also assume that
are mutually independent. We
also assume that
![]() ,
, ![]() ,
, ![]() , and
, and ![]() are
unknown. We do not assume that
are
unknown. We do not assume that
![]() . Let
. Let ![]() denote the difference in population means, sometimes called the
shift parameter.
denote the difference in population means, sometimes called the
shift parameter.
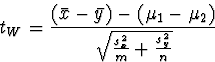
The distribution of this Welch's test statistic is approximately a t-distribution with the following number of degrees of freedom:
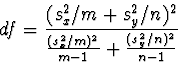
Remarks: When m=n (i.e. when the sample sizes are equal), tW equals Student's 2-sample t-statistic. The Welch test typically uses fewer degrees of freedom than the Student test.
A ![]() -level confidence interval for
-level confidence interval for
![]() is
is
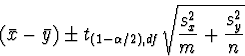
where ![]() is the critical value.
is the critical value.