1.

: Probabilities are usually between 0 and 1, but can be any number. 4lFalse: Probabilities must be between and 1.

F : For inferences in a regression model with p=3 predictor variables and an intercept, use the t distribution with n-1 degrees of freedom. 4lFalse: The degrees of freedom are n-3-1.

F : A P-value is a parameter. 4lFalse: The P-value is a statistic.

F : When testing a null hypothesis H₀: p = p₀ about a population

$$\sqrt{p_0(1-p_0)/n}$$ 4lTrue.

F : With ``before and after'' data, one should use the two sample methods described in section 7.2 of the text, with one sample being the before data and the other being the after data. 4lFalse: One should use matched pair methods from section 7.1

F : If the correlation is high, then it is not necessary to check the validity of a regression with scatterplots and residual plots. 4lFalse: There may still be violation of assumptions.

F : A statistic is an unknown quantity associated with the population. 4lFalse: A statistic is a quantity computed from the data.

F : The probability of exactly 2 heads in 4 independent flips of a fair coin is 0.5. 4lFalse: From Table B the probability is 0.3750.

: The P-value for a 2 sided test is 1-C where C is the confidence level of a confidence interval. 4lFalse: The Confidence level is not determined from the data, while the P-value is.

$$\beta_0 + \beta_1 x_i + \epsilon_i$$ F : ANOVA F-statistic is the square of the t-statistic for testing the Null Hypothesis that the slope is . 4lTrue. See p. 658.

2. [30 points] (Possible Final Project.) A local radio station KWHY claims they play more music than another station KNOT. A statistician decides to test this claim. He picks 50 random times during the week for each station and switches to that station and determines if they are playing music at exactly the time he switches the station on. He finds that KWHY is playing music at 22 out of the 50 times, and KNOT is playing music 28 out of the 50 times.

(a) What null and alternative hypotheses should the statistician test? Explain.

Solution: Let p₁ be the proportion of time KWHY plays music and p₂ the proportion for KNOT. The null hypothesis is clearly

H₀ : p₁ = p₂,

i.e., no difference. Now, what alternative? Clearly it is a one sided problem - KWHY claims to play more music, not just a different proportion of music. We could make the alternative hypothesis

H₁ : p₁ > p₂ .

Then, if we reject the null hypothesis, then we have strong evidence that KWHY's claim is true. On the other hand, if we are interested in disproving KWHY's claim, we could make the alternative

H₁ : p₁ < p₂ ,

i.e., that KWHY actually plays less music than KNOT.

The statistician wishes to test KWHY's claim, so he should use the first one.

(b) Compute the appropriate test statistic and P-value, and determine if there is significant evidence against the claim made by KWHY.

Solution: The sample porportions are

$$\hat{p}_1 = 22/50 = 0.44, \quad \hat{p}_2 = 28/50 = 0.56 .$$

The pooled proportion is

$$\hat{p}_0 \; = \; (22+28)/(50+50) \; = \; 0.50 .$$

The pooled standard error is

$$s_p \; = \; \sqrt{\hat{p}_0 (1- \hat{p}_0 ) (1/n_1 + 1/n_2 )} \; = \; \sqrt{.5*.5/(25)} \; = \; 0.10 .$$

The z statistic is

$$z \; = \; \frac{\hat{p}_1 - \hat{p}_2 }{s_p} \; = \; \frac{.44 - .56}{.10} \; = \; -1.2 .$$

We would reject the null hypothesis for large values of z, so the P-value is the area to the right of -1.2, which is 1-.1151 = .8849. Clearly, the null hypothesis is not rejected. There is not strong evidence for KWHY's claim. Since KNOT was playing music more often at the random times selected by the statistician, the evidence is against the claim made by KWHY. The test statistic

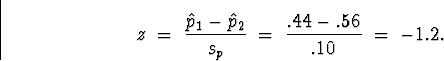
3. [30 points] The director of information services at a cool school in the south central US believes that using computerized foreign language instruction is superior to the old method with human instructors. After his method is implemented, he makes his case to the administration with results on a standardized test of fluency for a particular language. On the year before his method was implemented, there were 49 students who completed Mongolian 101 and 102, and their average score on the test was 38 with a standard deviation of 14. In the year that the computerized method was implemented, 16 students completed both semesters of introductory Mongolian. Their average score on the standardized test was 50 with a standard devation of 24.

The Information Services Director says that the data show a statistically significant increase in scores for the computer taught students vs. the human taught students.

(a) Assuming that the data are independent samples from the populations of human taught and computer taught foreign language students, verify the IS Director's claim of statistical significance.

Solution. Let $\mu_1$ be the true average score of students taught by the old method, and $\mu_2$ the population average of students taught by the new method. We wish to test

$$H_0 : \mu_1 = \mu_2 \quad vs. \quad H_A : \mu_1 < \mu_2 .$$

The t statistic is

The degrees of freedom we use is the smaller of n₁-1 = 49-1 and n₂ -1 = 14-1, i.e. we use 13 d.f. We reject for large values of t. Using Table E with 13 d.f., we see that the observed value is between 1.782 and 2.179 corresponding to tail areas 0.05 and 0.025. So, the result is significant at the usual 0.05 significance level.

(b) What's wrong with this picture? Comment from the point of view of proper statistical experimental design and validity of assumptions.

Solution. Clearly we cannot be certain that the results we observed are only due to the differences in instructional style. There may be other factors - maybe the students in the class with the new method were simply better at learning the language, for some reason. The proper way to design such an experiment is to randomly assign students to one of two sections, one using the new method and one using the old method. Then any observed differences are either due to chance or to actual differences.

One thing that looks problemmatic here is that so few students finished the year under the new program vs. the old one (14 vs 49). Perhaps students didn't like the new program and dropped out.

4. [35 points] A random sample of 199 married British women are asked their height (in mm.) and age of marriage. (Note from D. Cox: I am not making this up. This is real data from a real sample.) A few refuse to reply to one or the other question, leaving 195 for which we have data. Below are given

1)

the output of a regression analysis of these data with age of marriage as the dependent or response variable and height as the explanatory or predictor variable;

2)

a plot of the residuals vs. x_i's.

3)

a normal quantile plot of the residuals.

See last page for the plots. Use this information to answer the questions that follow.

Output from Stat Package:

Residual Standard Error = 5.6351,  Multiple R-Square = 0.0062
N = 195,  F-statistic = 1.2114 on 1 and 193 df, p-value = 0.2724

              coef std.err  t.stat p.value
Intercept  36.7218 10.3271  3.5559  0.0005
        X  -0.0071  0.0064 -1.1006  0.2724

(a) What is the predicted age of marriage for a woman who is 2000 mm. tall?

Solution. Plugging in x = 2000 to the fitted regression equation:

$$\hat{\beta}_0 + \hat{\beta}_1 x \; = \; 36.7218 -0.0071 * 2000 \; = \; 22.52 .$$

(b) According to the fitted regression model, do taller women tend to marry earlier or later?

Solution. The slope -0.0071, so the taller a woman is, the younger she will marry according to this fitted regression equation.

(c) Comment on how well or poorly the regression model fits these data. Use all available information.

Solution. The residual plot on the final page shows a few large residuals. This suggests the error distribution is skewed right. This is also born out by the Normal quantile plot of the residuals. We see that the actual values are above the line on the right (i.e. larger than expected from if the errors were normal) and above the line on the left. Thus, the assumption of normally distributed errors is questionable.

(d) A social scientist claims these data indicate there is no evidence that a woman's height has any bearing on the age at which she marries. A skeptic criticizes this conclusion, claiming, ``There is evidence the assumptions of the regression model are violated.'' Discuss the pros and cons of each point of view.

Solution. The P-value for the regression is 0.2724, so there is not significant evidence of a relationship between height and age of marriage, as the social scientist claims. However, the skeptic also has a point - since the error seem to have a distribution which is skewed to the right, there may have been one or more outlying values which messed up the regression. The jury is still out.

5. [10 points] A random sample of 100 students at an exclusive, snobby, elitist private college on the east coast are asked their beliefs about whether or not sexual harassment is prevalent at their school. The results are summarized in the table below.

1cPrevalent 1cNot Prevalent 1c|Don't Know 1cTotal

Male 8 30 12 50

Female 12 10 28 50

Total 20 40 40 100

(a) What is the value of Pearson's Chi-squared statistic for this table?

Solution.

Sex Belief Obs. O Exp. E (O-E)²/E

male prev 8 10 .4

not 30 20 5

don't know 12 20 3.2

female prev 12 10 .4

not 10 20 5

don't know 28 20 3.2

2|c||Total 100 100 17.2

The value of $\chi^2$ is 17.2 as indicated by the calculation above.

(b) Is there a statistically significant difference of opinion on the sexual harassment issue between the two genders?

The degrees of freedom here is (2-1)(3-1) = 2. The largest value in Table G for 2 d.f. is 15.20, corresponding to a significance level of 0.0005. Therefore, the P-value if < 0.0005, and there is a significant difference.

6. [20 points] Below is the 5 number summary of the age of marriage of the women in the data set described in the previous problem.

Five Number Summary:
Min       Q1        Med       Q3       Max
16        22         24       27        52

(a) Sketch a (density) histogram of the age of marriage using the available information.

Solution. The histogram is floating around on some page.

  

Figure 1: Histogram for Problem 6.

(b) Which of the following do you think is probably true about these data: the mean and median are about the same; the mean is somewhat greater than the median; the mean is somewhat less than the median. Explain your answer.

Solution. The histogram shows the distribution to be quite skewed to the right. So we expect the mean to be bigger than the median.

7. [25 points] A baseball player has a lifetime record of making hits in 30% of his ``at-bats'' (that is, his batting average is .300). In the first playoff game, he has 7 at-bats (the game went 19 innings) but makes only 1 hit. The player is depressed about this and fears he is in a slump but the coach says it is just chance variation.

(a) State some more or less reasonable assumptions that will allow you to compute a probability that the player makes 1 or fewer hits in 7 attempts, and compute that probability.

Solution. Assume that whether he makes a hit is independent between the at-bats, and the probability is always .3 for a hit on a single given at-bat. Then, the number of hits in 7 at-bats is a B(7,.3) random variable. The probability of or 1 hits by Table B is

$$0.0824 + 0.2471 \; = \; 0.3295 .$$

(b) Comment on the validity of the coach's claim that the player's performance in the first playoff game is chance variation.

Solution. There is about a 1 in 3 chance that in 7 at bats the player will get 1 or 0 hits, under our assumptions, so it is not uncommon. The coach could be right.