Solution to Exercise 7.04.

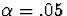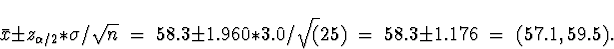
  (a) Using the formula on p. 282 with $\alpha = .05$,

$$\bar{x}\pm z_{\alpha/2} * \sigma/\sqrt{n} \; = \; 58.3 \pm... ...* 3.0/\sqrt(25) \; = \; 58.3 \pm 1.176 \; = \; (57.1,59.5) .$$

Note that we rounded off 1.176 to 1.2 for the last computation since 58.3 has only one significant digit after the decimal point.

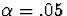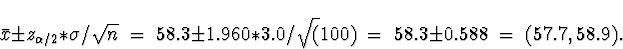
(b) Using the formula on p. 282 with $\alpha = .05$,

$$\bar{x}\pm z_{\alpha/2} * \sigma/\sqrt{n} \; = \; 58.3 \pm... ... 3.0/\sqrt(100) \; = \; 58.3 \pm 0.588 \; = \; (57.7,58.9) .$$

Note that interval width is 1/2 of part (a).

(c) Using the formula on p. 282 with 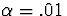$\alpha = .01$,

$$\bar{x}\pm z_{\alpha/2} * \sigma/\sqrt{n} \; = \; 58.3 \pm... ...3.0/\sqrt(100) \; = \; 58.3 \pm 0.7728 \; = \; (57.5,59.1) .$$

Note that we have a somewhat wider interval than in part (b) in order to get more confidence.

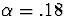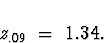
(d) With $\alpha = .18$,

$$z_{.09} \; = \; 1.34 .$$

This comes from Table A.3 which gives

$$\Phi(1.34) \; = \; 0.9099 \; = \; 1 - .0901 ,$$

which is the closest we can get. Thus,

$$\bar{x}\pm z_{\alpha/2} * \sigma/\sqrt{n} \; = \; 58.3 \pm... ... 3.0/\sqrt(100) \; = \; 58.3 \pm 0.402 \; = \; (57.9,58.7) .$$

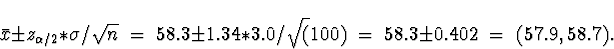
(e) The width of a 95% CI in this case is

$$2*1.960*3.0/\sqrt{n} \; = \; 1.0 .$$

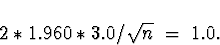
Solving for n gives

$$n \; = \; (2*1.960*3.0)^2 \; = \; 138.2976 .$$

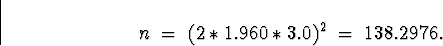
We would use n = 139. Of course, one could also use the formula on the bottom of p. 283 with w = 1.0.