

Next: About this document ...
Up: No Title
Previous: Solution to Exercise 7.14.
Using the formula on p. 293, the large sample upper
confidence bound for 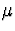 is
is
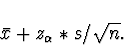
As in all the formulae for confidence bounds for a
proportion p, we replace 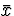 by
by 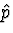 and
s by
and
s by 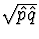 . We have
. We have

Also, z.01 = 2.326 (for 99% confidence). Thus,
our 99% upper confidence bound is
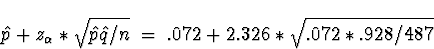
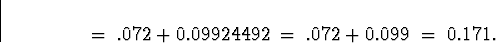
Dennis Cox
3/24/2001
![]()
![]()
![]()
![]()