

Next: Binomial Approx. to Hypergeo.;
Up: No Title
Previous: The hypergeometric distribution:
Suppose we still have the population of size N with M
units labelled as ``success'' and N-M labelled as ``failure,''
but now we take a sample of
size n is drawn with replacement.
Then, with each draw, the units remaining to be drawn
look the same: still M ``successes'' and
N-M ``failures.'' Thus, the probability of drawing
a ``success'' on each single draw is
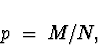
and this doesn't change. When we were drawing without
replacement, the proportions of successes would change,
depending on the result of previous draws. For example,
if we were to obtain a ``success'' on the first draw,
then the proportion of ``successes'' for the second draw
would be (M-1)/(N-1), whereas if we were to obtain a ``failure''
on the first draw the proportion of successes for the second
draw would be M/(N-1).
The random
variable Y is defined as the number of ``successes'' in
the sample, when we are drawing with replacement.
Then Y is a binomial random variable:

The probability mass function for Y is
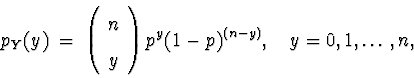
and otherwise.
Proposition:
If the population size 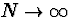 in
such a way that the proportion of successes
in
such a way that the proportion of successes 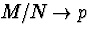 ,and n is held constant,
then the hypergeometric probability mass function approaches the binomial
probability mass function:
,and n is held constant,
then the hypergeometric probability mass function approaches the binomial
probability mass function:
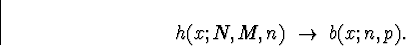
In practice, this means that we can approximate the hypergeometric
probabilities with binomial probabilities, provided 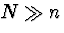 .As a rule of thumb, if the population size is more
than 20 times the sample size (N > 20 n), then we may use
binomial probabilities in place of hypergeometric probabilities.
.As a rule of thumb, if the population size is more
than 20 times the sample size (N > 20 n), then we may use
binomial probabilities in place of hypergeometric probabilities.
We next illustrate this approximation in some examples.


Next: Binomial Approx. to Hypergeo.;
Up: No Title
Previous: The hypergeometric distribution:
Dennis Cox
2/12/2001
![]()
![]()
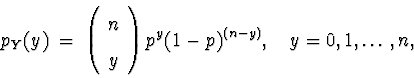
![]() in
such a way that the proportion of successes
in
such a way that the proportion of successes ![]() ,and n is held constant,
then the hypergeometric probability mass function approaches the binomial
probability mass function:
,and n is held constant,
then the hypergeometric probability mass function approaches the binomial
probability mass function:
![]()
![]() .As a rule of thumb, if the population size is more
than 20 times the sample size (N > 20 n), then we may use
binomial probabilities in place of hypergeometric probabilities.
.As a rule of thumb, if the population size is more
than 20 times the sample size (N > 20 n), then we may use
binomial probabilities in place of hypergeometric probabilities.