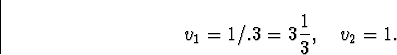
Solution to Exercise 3.3.

Problem Statement: For each of the models of exercise 3.1 and also for the following models, state whether it is (a) stationary; (b) invertible.

Solution: These are all ARMA models, so stationarity holds if and only if the roots of the AR equation $\phi(w) = 0$ are all outside the unit circle, and invertibility if and only if the roots of the MA equation $\theta (w) = 0$ are all outside the unit circle.

Note: The authors write 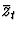$\bar{z}_t$ all the time to emphasize that you have to take out the mean for these models. We will just write Z_t and assume everything is mean .

Model 1:

$$Z_t - 0.6 Z_{t-1} \; = \; a_t .$$

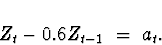
The root(s) of the autoregressive characteristic equation

$$1- 0.6 v \; = \; 0 ,$$

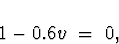
is(are) 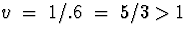$v \; = \; 1/.6 \; = \; 5/3 \gt 1$, outside the unit circle. Therefore, the process is stationary.

The root(s) of the moving average characteristic equation

$$1 \; = \; 0 ,$$

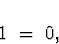
form an empty set, thus all roots are vacuously outside the unit circle. Put differently (in the language that was used in lecture), there are no roots of 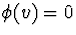$\phi (v) = 0$ on or in the unit circle. Therefore, the process is invertible.

Model 2:

$$Z_t \; = \; a_t -1.3 a_{t-1} + 0.4 a_{t-2} .$$

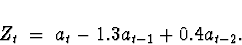
The root(s) of the autoregressive characteristic equation

$$1 \; = \; 0 ,$$

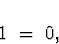
form an empty set, thus all roots are vacuously outside the unit circle. Put differently (in the language that was used in lecture), there are no roots of 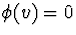$\phi (v) = 0$ on or in the unit circle. Therefore, the process is stationary.

The roots of the moving average characteristic equation

$$1 -1.3 v + 0.4 v^2 \; = \; 0 ,$$

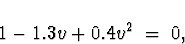
can be determined by factoring:

$$(1 - .5 v)(1 - .8 v) \; = \; 0$$

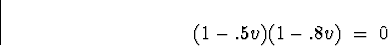
which gives

$$v_1 = 1/.5 = 2 , \quad v_2 = 1/.8 = 1.25 .$$

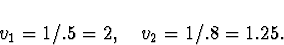
Both roots are outside the unit circle. Therefore, the process is invertible.

Model 3:

$$Z_t - 0.6 Z_{t-1} \; = \; a_t -1.3 a_{t-1} + 0.4 a_{t-2} .$$

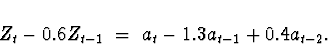
The root of the autoregressive characteristic equation

$$1- 0.6 v \; = \; 0 ,$$

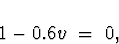
is 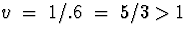$v \; = \; 1/.6 \; = \; 5/3 \gt 1$, outside the unit circle. Therefore, the process is stationary.

The moving average operator is the same as in Model 2, so the process is invertible.

Model 4:

$$Z_t - 1.5 Z_{t-1} + 0.6 Z_{t-2} \; = \; a_t .$$

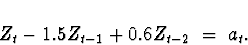
The roots of the autoregressive characteristic equation

$$1- 1.5 v + 0.6 v^2 \; = \; 0 ,$$

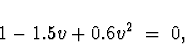
are

The modulus squared of these complex conjugate roots is

$$\vert v_+ \vert^2 \; = \; \vert v_- \vert^2 \; = \; 1.25^2 + (\pm \sqrt{15}/12)^2 \; \gt \; 1.25^2 \; \gt \; 1 ,$$

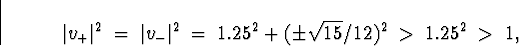
outside the unit circle. Therefore, the process is stationary. (One can determine this without computing the roots, once it is known that the roots are complex conjugates. Recall that the product of reciprocal roots is the modulus squared and equal to the coefficient of v², namely 0.6 in this case, so the modulus squared is 1/0.6 > 1.)

The process is invertible as in Model 1.

Model 5:

$$Z_t - Z_{t-1} \; = \; a_t - 0.5 a_{t-1} .$$

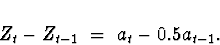
The root of the autoregressive characteristic equation

$$1- v \; = \; 0 ,$$

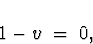
is 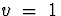$v \; = \; 1$, on the unit circle. Therefore, the process is not stationary.

The root of the moving average characteristic polynomial

1 - 0.5 v = 0 ,

is v = 2, outside the unit circle. Therefore, the process is invertible.

Model 6:

$$Z_t - Z_{t-1} \; = \; a_t -1.3 a_{t-1} + 0.3 a_{t-2} .$$

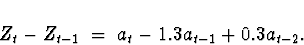
The root of the autoregressive characteristic equation

$$1- v \; = \; 0 ,$$

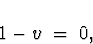
is 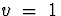$v \; = \; 1$, on the unit circle. Therefore, the process is not stationary.

The roots of the moving average characteristic equation

$$1 -1.3 v + 0.3 v^2 \; = \; 0 ,$$

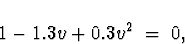
can be determined by factoring:

$$(1 - .3 v)(1 - v) \; = \; 0$$

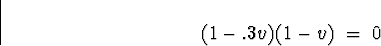
which gives

$$v_1 = 1/.3 = 3 \frac{1}{3} , \quad v_2 = 1 .$$

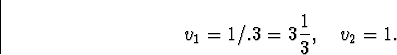
One root is outside the unit circle but one is on the unit circle. Therefore, the process is not invertible.