Statistical Methods

We will use the Minitab statistical package. Since there are so many predictor variables, we utilized variable selection methods. The first variable selection procedure is Stepwise..., the second is Best Subsets..., and the third is Cross-Validation. We had to implement the last method by hand in Minitab as it is not available as a menu item. The stepwise method is described in the text (section 11.10, p. 531). It starts with no variables and uses repeated testing of hypotheses to see if there is a significant variable that can be entered or a variable already in the model which has lost statistical significance and can be deleted. While it is not an unreasonable procedure, it lacks any formal statistical justification. It does seem to work well in many examples in practice. For the best subsets method, we select the regression model which is displayed and has the smallest value of $C_p$. This statistic is an indicator of which model will predict best in new data. It is based on an assumption of independent data and constant error variance. The formula and further discussion may be found in the text.

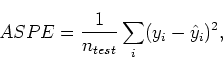
Cross-validation involved splitting the data into two subsets. The two subsets are called the training data and the validation or test data. The training data is used to estimate the coefficients of the regression model. The test data are used to compute the average squared prediction error for each regression model:

$$ASPE = \frac{1}{n_{test}} \sum_i (y_i - \hat{y}_i)^2 ,$$

where $n_{test}$ is the number of observations in the test data, $y_i$ denotes a response variable value in the test data (the sum is only over the observations in the test data), and $\hat{y}_i$ is the predicted value for $y_i$ from the regression model. Of course, the regression coefficients used to construct $\hat{y}_i$ are based only on the training data.

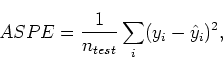
To split the data into training and test data, a random subsample of the data should be used. We did this by first generating a column of random numbers the same length as the data, sorting on the random numbers (so the data are in essentially random order), and then selecting the first 63 observations for the test data. These were cut and paste into new columns. One should select a relatively small sample for the test data so that most of the data can be used for estimating the regression coefficients. Also, one should try for at least 30 observations in the test data to provide a reasonable stable and accurate estimate of the ASPE. This is why cross validation is only reasonable for large data sets.

We ran the cross validation on all the regression models selected by the Best Subsets method so that we could compare with $C_p$. This was done by running the Regression function on each model, predicting at the values of the predictor variables in the test data set, and computing the ASPE. This was admittedly rather tedious. However, once we got started it was not too bad since it was fairly quick to change the predictor variables in the regression dialogue box. Also, we deleted the column of predicted values after each run so that the next column would appear in the same place and the ASPE calculation (done in the calc menu) never had to be changed (simply pull down the calculator and check OK). The value of ASPE after each run was cut and paste into a colum of values. We also deleted most of the output from the regression command.

The Stepwise and Best Subsets methods were run originally on the entire data set using the original origin variable. After that, a new data set was constructed by first creating the origin indicator variables and the two methods were run again. Finally, we dropped the variables cylinder (number of cylinders) and acc (acceleration) since neither Stepwise nor Best Subsets wanted them (I had to decrease the size of my data set because of the limits of the student edition of Minitab), selected the random subset of test data, and reran the two methods on the training data as well as cross validation.