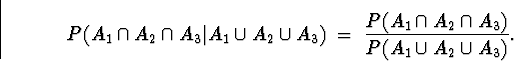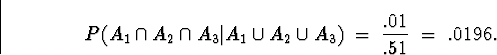

Next: Solution to Exercise 2.64.
Up: No Title
Previous: Solution to Exercise 2.36.
Problem Statement:
In Exercise 13. Ai =  awarded project i
awarded project i  . for i = 1,
2,3. Use the
probabilities given there to compute following probabilities:
. for i = 1,
2,3. Use the
probabilities given there to compute following probabilities:
(a)
P(A2 | Al)
Solution:
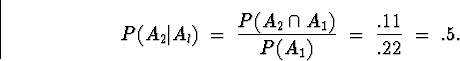
(b)
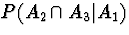
Solution:
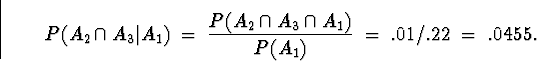
(c)
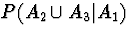
Solution:
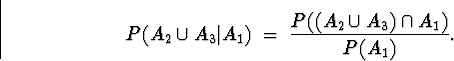
It seems we didn't compute the probability in the numerator yet, so it's
back to the Venn diagrams, shown below.
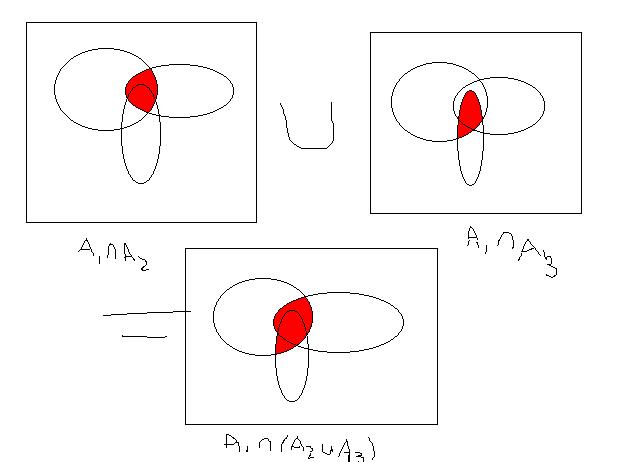
Figure 3:
Venn Diagram for part (c). The colored part is
 . The red part is
. The red part is
 .
.
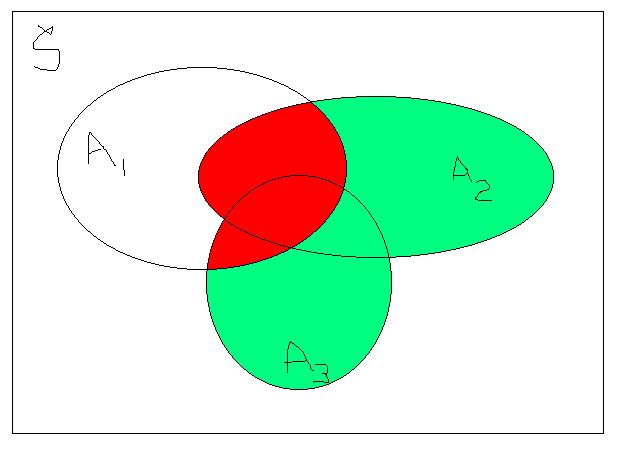 |
Also below is my crude attempt to use Venn diagrams to show that
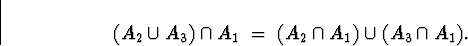
(There is a distributive law at work here. If you know what it
means, you can probably check (or already know) that both union
and intersection distribute over each other.)
Figure 4:
Venn Diagram for part (c) demonstrating that
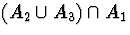 =
=
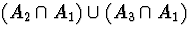 .
.
 |
Given this identity, we can make the calculation using the
information provided in conjunction with the proposition on
p. 62:
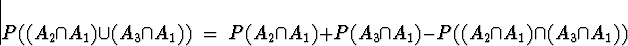
Plugging in the numbers, we have
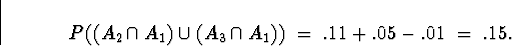
Hence,
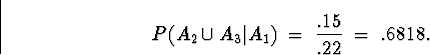
(d)
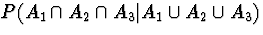 .Express in words probability you
have calculated.
.Express in words probability you
have calculated.
Solution:
Well, it's pretty easy to see that
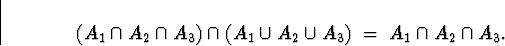
This follows since
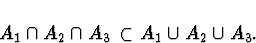
Draw Venn diagrams if you have to, but basically the
event that all three happen is contained in the event
that at least one happens.
Hence,
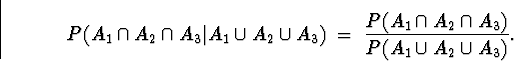
We already figured out the denominator in part (c)
of Problem 13, and the numerator was already given, so
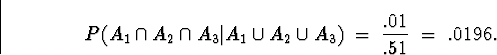
In words, we have calculated the conditional probability
that the firm wins all 3 projects given that they win at
least one.


Next: Solution to Exercise 2.64.
Up: No Title
Previous: Solution to Exercise 2.36.
Dennis Cox
2/4/2001
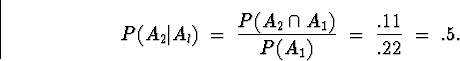
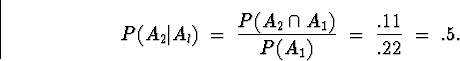
![]()
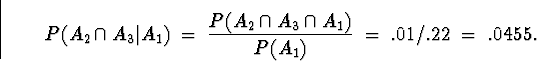
![]()
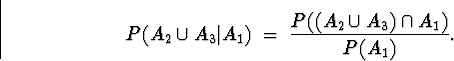
![]()
![]()
![]()
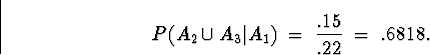
![]() .Express in words probability you
have calculated.
.Express in words probability you
have calculated.
![]()
![]()