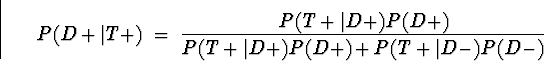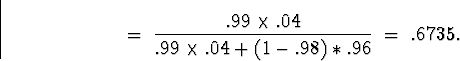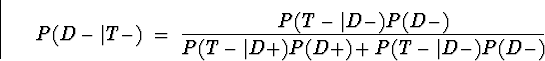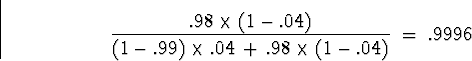

Next: About this document ...
Up: No Title
Previous: Solution to Exercise 2.54.
Problem Statement:
In Example 2.30, suppose that the incidence rate for disease
is 1 in 25 rather than 1 in 1000. What then is the probability of
a positive test result? Given that the test result is positive, what
is the probability that the individual has the disease? Given a
negative test result, what is the probability that the individual
does not have the disease?
Solution:
The author is changing the prevalence (percentage of persons in
the population who have the disease) from .001 to .04 = 1/25.
(``Incidence'' actually means something else, and shouldn't
have been used here.) We shall use the notations given in
class, i.e. D+ means the event that a person chosen at
random is positive for the disease, and T+ means that such
a person is positive for the test. The same notations with
the minus signs denote the complementary events; e.g. D-
means negative for disease. We are given that the
sensitivity and specificity are
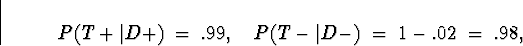
respectively. The prevalence is P(D+) = .04, so
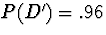 . Applying Bayes Theorem, the positive
predictive power of the test is
. Applying Bayes Theorem, the positive
predictive power of the test is
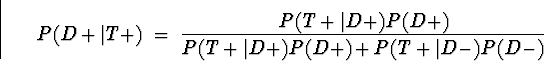
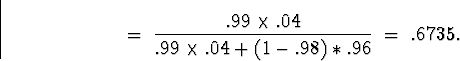
The negative predictive power is
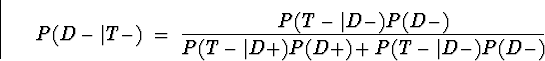
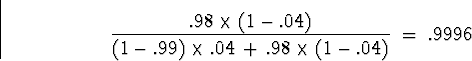
Because the disease is so rare, the negative
predictive power is very high.


Next: About this document ...
Up: No Title
Previous: Solution to Exercise 2.54.
Dennis Cox
2/4/2001
![]()