Solution to Exercise 4.32.

  Letting X denote the substrate concentration in mg/cm³, we are given that

$$X \sim N(.30,(.06)^2).$$

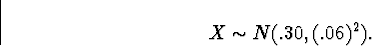
Below, Z = (X-.30)/.06 we be N(0,1).

(a)

$$P[ X \ge .25] \; = \; P \left[ Z \ge \frac{.25 - .30}{.06} ... ... \ge -.83 ] \; = \; 1 - \Phi(-.83) \; = \; 1 - .2033 = .7967 .$$

(b)

$$P[ X \le .10] \; = \; P \left[ Z \le \frac{.10 - .30}{.06} ... ...] \; = \; P[ Z \le -3.33 ] \; = \; \Phi(-3.33) \; = \; .0004.$$

(c) From Table 4.1 on p. 163, z_.05 = 1.645. Therefore, the 95'th percentile of the distribution of X is

$$(0.06)*1.645 + .30 \; = \; 0.3987 ,$$

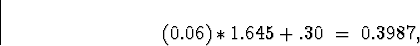
that is, the largest 5% of values are those above 0.3987.