Next: Solution to Exercise 4.59. Up: No Title Previous: Solution to Exercise 4.32.

Solution to Exercise 4.48.

The r.v. X is Bin(200,.1). We have

$\begin{displaymath} \min \{ np , n(1-p) \} \; = \; \min \{ .1 * 200 , .9 * 200 \} \; = \; 20 \gt 10,\end{displaymath}$

so the normal approximation to the binomial applies. We use

$\begin{displaymath} \mu \; = \; 20 , \quad \sigma \; = \; \sqrt{20*.9} \; = \; 4.242641 .\end{displaymath}$

(a) Applying the continuity correction,

$\begin{displaymath} P[ X \le 30 ] \; = \; P[ X \le 30.5 ] .\end{displaymath}$

The desired probability is approximately

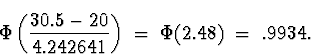
$\begin{displaymath} \Phi \left( \frac{30.5-20}{4.242641} \right) \; = \; \Phi(2.48) \; = \; .9934.\end{displaymath}$

(The exact value is .9905, to 4 decimal places. If you didn't use the continuity correction, you would get $\Phi(2.36) = .9909$ , which is actually closer in this case.)

(b) The continuity correction in this case is

$\begin{displaymath} P[ X < 30 ] \; = \; P[ X \le 29.5 ] .\end{displaymath}$

The desired probability is approximately

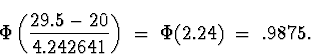
$\begin{displaymath} \Phi \left( \frac{29.5-20}{4.242641} \right) \; = \; \Phi(2.24) \; = \; .9875.\end{displaymath}$

(The exact value is .9837, to 4 decimal places. If you didn't use the continuity correction, you would get $\Phi(2.12) = .9830$ , which is again closer.)

(c) The continuity correction in this case is

$\begin{displaymath} P[ 15 \le X \le 25 ] \; = \; P[ 14.5 \le X \le 25.5 ] .\end{displaymath}$

The desired probability is approximately

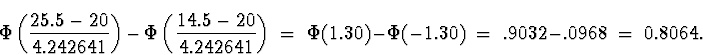
$\begin{displaymath} \Phi \left( \frac{25.5-20}{4.242641} \right) \, - \, \Phi ... ...Phi(1.30) - \Phi(-1.30) \; = \; .9032 - .0968 \; = \; 0.8064 .\end{displaymath}$

(The exact value is .8066, to 4 decimal places. If you didn't use the continuity correction, you would get $\Phi(1.18) -\Phi(-1.18) = .7620$ .Obviously, the continuity correction is helpful in this case.)

Dennis Cox
2/26/2001