Next: Solution to Exercise 4.74. Up: No Title Previous: Solution to Exercise 4.48.

Solution to Exercise 4.59.

Note that 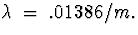$\lambda \; = \; .01386 / m.$ . The c.d.f. for X is

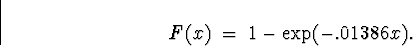
$\begin{displaymath} F(x) \; = \; 1 - \exp(-.01386 x) .\end{displaymath}$

(a)

$\begin{displaymath} P[ X \le 100 ] \; = \; 1- \exp(-1.386) \; = \; 0.7499 .\end{displaymath}$

$\begin{displaymath} P[ X \le 200 ] \; = \; 0.9375 .\end{displaymath}$

$\begin{displaymath} P[ 100 < X \le 200 ] \; = \; .9375 - .7499 \; = \; .1876 .\end{displaymath}$

(b) By the formulae on the bottom of p. 174,

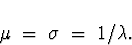
$\begin{displaymath} \mu \; = \; \sigma \; = \; 1/ \lambda .\end{displaymath}$

You can calculate this as 72.15, but we won't need it. We have

$\begin{displaymath} P[ X \gt \mu + 2 \sigma ] \; = \; P[ X \gt 3 / \lambda ] \;... ...[ - \lambda * (3/\lambda) ] \; = \; \exp[ -3] \; = \; 0.0498 .\end{displaymath}$

(c) Solving for F^-1 (.5):

$\begin{displaymath} 1 - \exp[ - \lambda x ] \; = \; .5 \; \Longrightarrow \; x \... ...\; - \log(.5)/\lambda \; = \; \log(2)/\lambda \; = \; 50.01 .\end{displaymath}$

Dennis Cox
2/26/2001