Solution to Exercise 4.84.

  The analysis was done in Minitab. Unfortunately, the CD in the back of the book didn't have this data set on it, so we had to type it into Minitab in C1.

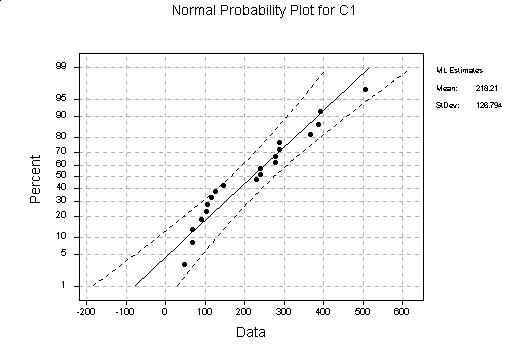
(a) The Normal probability plot appears below. The data are kind of ``clumped,'' but otherwise are more or less straight. There isn't strong evidence that the data are not normal.

(b) We will explain the Weibull probability plots in a manner which make things clearer than in the text, hopefully. We first show the Weibull distribution can be obtained from an Exponential distribution by a power transformation. Let

$$Y \; \sim \; Weibull(\alpha,\beta) ,$$

so the cumulative distribution function is

$$F_Y (y) \; = \; P[ Y \le y ] \; = \; 1 - \exp(-(y/\beta)^{\alpha}) \; = \; G((y/\beta)^{\alpha})$$

where G(z) (say) is the c.d.f. of the exponential with parameter 1:

$$G(z) = 1 - \exp(-z).$$

Therefore, you can take the exponential quantiles

x_i = G^-1 ( (i-.5)/n )

and plot against them, but if y₍₁₎ < y₍₂₎ < $\ldots$ < y_(n) are the ordered data values ("order statistics") from data you think are Weibull, you will have a power relationship

$$(y_{(i)}/\beta)^{\alpha} \approx x_i$$

$$y_{(i)} \approx \beta*x_i^{(1/\alpha)}$$

Taking log's of both sides, we get

$$\log y_{(i)} \approx (1/\alpha)*\log x_i + \log \beta$$

so on log-log paper, you get a straight line, with slope $1/\alpha$ and intercept $\log \beta$.

So, the plan is to use exponential (with parameter 1) quantiles:

$$(i-.5)/n = 1-\exp(x_i) \Longrightarrow x_i = - \log(1- (i-.5)/n)$$

quantiles and do log-log plotting.

These (theoretical) quantiles for the exponential distribution are obtained by solving

$$(i-.5)/20 \; = \; 1 - e^{-x_i} .$$

Solving in steps:

$$1- (i-.5)/20 \; = \; e^{-x_i}$$

$$x_i \; = \; - \log \left( 1- (i-.5)/20 \right) .$$

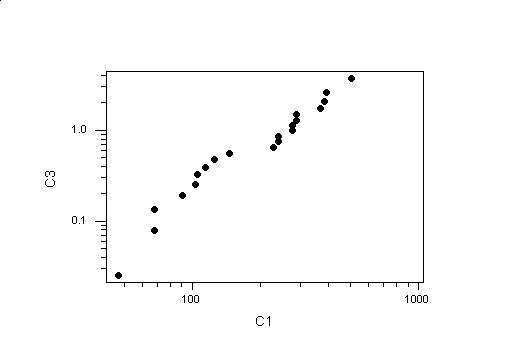
In order to do this in Minitab, we went to Calc -> Make Patterned Data -> Simple Sets of Numbers and stored the ``patterned data'' in C2, the data being ``First Value'' .5 to ``Last Value'' 19.5 in steps of 1 (this is (i-.5)/20 as i ranges from 1 to 20). Then we went back to the ``Calc'' menu, selected Calculator, and made C3 equal to - log(1-C2/20). Then we went to the ``Graph'' menu, selected ``Plot'', made the X variable C1 (the data) and the Y variable C3 (the theoretical quantiles) and selected ``Options'' to transform both axes by ``Logarithm.'' This produced the plot in the figure below. This looks about like a straight line, so it seems that the Weibull distribution is also a possible model for these data.

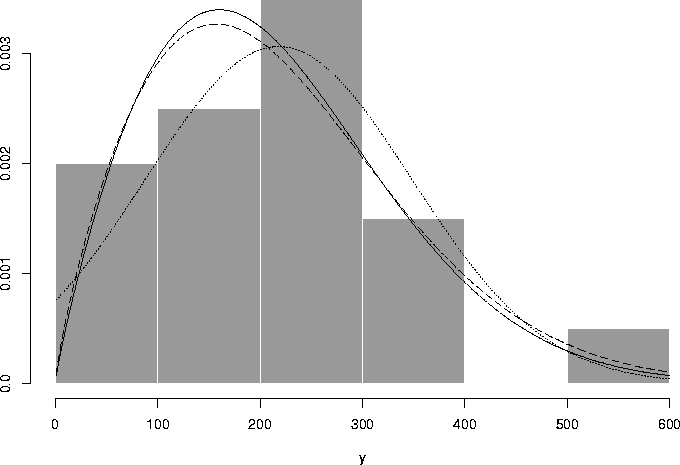
POSTSCRIPT: In order to figure this out, I plotted the histogram and overlaid the plots of the densities of the normal distribution (with parameters $(\mu,\sigma^2)$ equal to the the sample mean and variance $(\bar{y}, s^2)$) and the Weibull density (with parameters determined by fitting a straight line to the probability plot, and also by maximum likelihood). These appear below. It appears that neither model fits very well, in fact. The normal model is clearly untenable in this example as so much of the probability is on values less than 0. Using the estimated parameters, the probability of getting a value < 0 is 0.0467. Part of the problem is the small sample size.

  

Figure 1: Density histogram for the data along with plots of fitted densities. The solid curve is the Weibull with parameters $\alpha = 1.868$ and $\beta = 241.60$, which were determined by fitting a line to the data (x_i,y_(i)) used to produce the Weibull probability plot. The slashed line curve which is close to the solid curve is the maximum likelihood Weibull fit with estimated parameters $\alpha = 1.803$ and $\beta = 246.23$. The dotted curve is the normal density with $\mu = \bar{y} = 218.21$ and $\sigma = s = 130.09$.