

Next: Solution to Exercise 5.06.
Up: No Title
Previous: Solution to Exercise 4.84.
(a)
The assumed independence gives
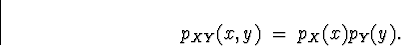
The results are shown in Table 2.
Table 1:
Table of joint probability mass function for this
exercise. Values of X appear in column 1 and
values of Y in row 1. For example,
pXY (1,4) = pX (1) pY (4) =
.3 * .2 = .06.
| |
|
1 |
2 |
3 |
4 |
| |
.300 |
.050 |
.025 |
.025 |
.100 |
| 1 |
.180 |
.030 |
.015 |
.015 |
.060 |
| 2 |
.120 |
.020 |
.010 |
.010 |
.040 |
(b)
Adding the values from the table:
![\begin{displaymath}
P[X \le 1 \, \& \, Y \le 1 ] \; = \;
p_{XY} (0,0) + p_{XY} (0,1) + p_{XY} (1,0) + p_{XY} (1,1)\end{displaymath}](img24.gif)
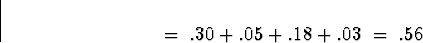
Computing the individual probabilities:
![\begin{displaymath}
P[X \le 1 ] \; = \; .5 + .3 \; = \; .8 ,\end{displaymath}](img26.gif)
![\begin{displaymath}
P[Y \le 1 ] \; = \; .6 + .1 \; = \; .7 ,\end{displaymath}](img27.gif)
and of course
![\begin{displaymath}
P[X \le 1 \, \& \, Y \le 1 ] \; = \;
P[X \le 1 ] * P[ Y \le 1 ] \; = \;
.8 * .7 = .56 .\end{displaymath}](img28.gif)
(c)
![\begin{displaymath}
P[X + Y = 0 ] \; = \; P[X = 0 \, \& \, Y = 0 ]
\; = \; p_{XY} (0,0) \; = \; .3 .\end{displaymath}](img29.gif)
(d)
![\begin{displaymath}
P[ X + Y \le 1 ] \; = \;
p_{XY} (0,0) + p_{XY} (0,1) + p_{XY} (1,0)\end{displaymath}](img30.gif)
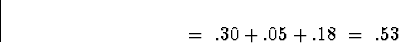


Next: Solution to Exercise 5.06.
Up: No Title
Previous: Solution to Exercise 4.84.
Dennis Cox
3/10/2001
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()