

Next:Solution
to Exercise 5.22.Up:No
TitlePrevious:Solution
to Exercise 5.02.
Solution to Exercise 5.06.
(a) The hint is that
![\begin{displaymath}P[ X=4 \, \& \, Y = 2 ] \; = \; P[ Y = 2 \vert X = 4 ] P [X = 4 ] .\end{displaymath}](img32.gif)
Note that this follows from the definition of conditional probability:
![\begin{displaymath}P[ Y = 2 \vert X = 4 ] \; = \; \frac{P[ X=4 \, \& \, Y = 2 ]}{P [X = 4 ]} .\end{displaymath}](img33.gif)
Now, if X = 4, that means 4 VCR's were purchased. We assume that
each customer who buys a VCR is independent of the others and has a probability
of 0.6 of buying the extended warranty. Thus, give X = 4, Y
is a Bin(4,.6) random variable. Hence,
![\begin{displaymath}P[ Y = 2 \vert X = 4 ] \; = \; \left( \begin{array}{c} 4 \\ 2 \end{array} \right).6^{2} (1-.6)^2\end{displaymath}](img34.gif)
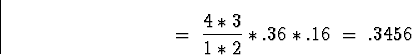
and hence
![\begin{displaymath}P[ X=4 \, \& \, Y = 2 ] \; = \; .3456*.25 = .0864 .\end{displaymath}](img36.gif)
Note: this should be .3456*.15 = 0.05184. Sorry about
the mistake. It's easier to correct it this way than put it in the equation.
(c) We will do part (c) next because we can use some of the results
from part (c) for part (b). Of course always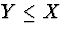 ,
so we can start the table of the joint p.m.f.:
,
so we can start the table of the joint p.m.f.:
Table 2: Beginning the table of the joint p.m.f.
| |
y=0 |
y=1 |
y=2 |
y=3 |
y=4 |
| x=0 |
.1 |
|
|
|
|
| x=1 |
.08 |
.12 |
|
|
|
| x=2 |
 |
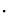 |
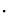 |
|
|
| x=3 |
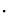 |
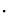 |
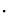 |
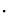 |
|
| x=4 |
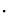 |
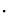 |
 |
 |
 |
The entries for x=0 and x=1 are easy:
![\begin{displaymath}P[X=1 \, \& \, Y=1] \; = \; P[Y=1 \vert X=1] P[X=1] \; = \; .6 * .2 \; = \; .12\end{displaymath}](img39.gif)
Now if X=2, Y has a (conditional) Bin(2,.6) distribution.
Thus,
![\begin{displaymath}P[ Y = 0 \vert X = 2 ] \; = \; \left( \begin{array}{c} 2 \\ 0 \end{array} \right).6^{0} (1-.6)^2\end{displaymath}](img40.gif)
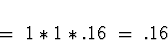
and
![\begin{displaymath}P[ Y = 1 \vert X = 2 ] \; = \; \left( \begin{array}{c} 2 \\ 1 \end{array} \right).6^{1} (1-.6)^1\end{displaymath}](img42.gif)
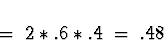
and finally
![\begin{displaymath}P[ Y = 2 \vert X = 2 ] \; = \; \left( \begin{array}{c} 2 \\ 2 \end{array} \right).6^{2} (1-.6)^0\end{displaymath}](img44.gif)
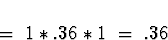
Multiplying these by .3 = P[X=2] gives the nonzero entries
in the third row as .48, .144, and .108.
We give the results for the next two rows without the detailed calculations:
![\begin{displaymath}P[Y=y\vert X=3] \; = \; \left\{ \begin{array}{ccl}0.064 & ... ...& \mbox{if } y=2 \\ 0.216 & & \mbox{if } y=3\end{array} \right.\end{displaymath}](img46.gif)
These are multiplied by .25 = P[X=3] to obtain the nonzero
entries in the fourth row.
![\begin{displaymath}P[Y=y\vert X=4] \; = \; \left\{ \begin{array}{ccl}0.0256 &... ... \mbox{if } y=3 \\ 0.1296 & & \mbox{if } y=4\end{array} \right.\end{displaymath}](img47.gif)
These are multiplied by .15 = P[X=4] to obtain the nonzero
entries in the fifth row.
Table 3: Table of the joint p.m.f.
| |
y=0 |
y=1 |
y=2 |
y=3 |
y=4 |
| x=0 |
.1 |
|
|
|
|
| x=1 |
.08 |
.12 |
|
|
|
| x=2 |
0.48 |
0.144 |
0.108 |
|
|
| x=3 |
0.016 |
0.072 |
0.108 |
0.054 |
|
| x=4 |
0.00384 |
0.02304 |
0.05184 |
0.05184 |
0.01944 |
| sum |
0.24784 |
0.35904 |
0.26784 |
0.10584 |
0.01944 |
We have summed the columns to obtain the marginal p.m.f. for
Y,
e.g. pY (2)  0.26784.
0.26784.
(b)
![\begin{displaymath}P[X=Y] \; = \; p_{XY} (0,0) +p_{XY} (1,1) +p_{XY} (2,2) +p_{XY} (3,3) +p_{XY} (4,4)\end{displaymath}](img49.gif)
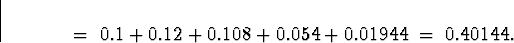


Next:Solution
to Exercise 5.22.Up:No
TitlePrevious:Solution
to Exercise 5.02.
Dennis Cox
3/10/2001
![]()
![]()
![\begin{displaymath}P[ Y = 2 \vert X = 4 ] \; = \; \frac{P[ X=4 \, \& \, Y = 2 ]}{P [X = 4 ]} .\end{displaymath}](img33.gif)
![\begin{displaymath}P[ Y = 2 \vert X = 4 ] \; = \; \left( \begin{array}{c} 4 \\ 2 \end{array} \right).6^{2} (1-.6)^2\end{displaymath}](img34.gif)
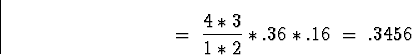
![]()
![]() ,
so we can start the table of the joint p.m.f.:
,
so we can start the table of the joint p.m.f.:
![]()
![\begin{displaymath}P[ Y = 0 \vert X = 2 ] \; = \; \left( \begin{array}{c} 2 \\ 0 \end{array} \right).6^{0} (1-.6)^2\end{displaymath}](img40.gif)
![]()
![\begin{displaymath}P[ Y = 1 \vert X = 2 ] \; = \; \left( \begin{array}{c} 2 \\ 1 \end{array} \right).6^{1} (1-.6)^1\end{displaymath}](img42.gif)
![]()
![\begin{displaymath}P[ Y = 2 \vert X = 2 ] \; = \; \left( \begin{array}{c} 2 \\ 2 \end{array} \right).6^{2} (1-.6)^0\end{displaymath}](img44.gif)
![]()
![\begin{displaymath}P[Y=y\vert X=3] \; = \; \left\{ \begin{array}{ccl}0.064 & ... ...& \mbox{if } y=2 \\ 0.216 & & \mbox{if } y=3\end{array} \right.\end{displaymath}](img46.gif)
![\begin{displaymath}P[Y=y\vert X=4] \; = \; \left\{ \begin{array}{ccl}0.0256 &... ... \mbox{if } y=3 \\ 0.1296 & & \mbox{if } y=4\end{array} \right.\end{displaymath}](img47.gif)
![]() 0.26784.
0.26784.
![]()
![]()