

Next: Solution to Exercise 5.30.
Up: No Title
Previous: Solution to Exercise 5.06.
We have reproduced the table of the joint p.m.f. but
summed the rows and columns to get the marginal p.m.f.'s.
Table 4:
Table of joint p.m.f. with marginal
p.m.f.'s shown.
| |
y=0 |
y=5 |
y=10 |
y=15 |
pX |
| x=0 |
0.02 |
0.06 |
0.02 |
0.10 |
0.20 |
| x=5 |
0.04 |
0.15 |
0.20 |
0.10 |
0.49 |
| x=10 |
0.01 |
0.15 |
0.14 |
0.01 |
0.31 |
| pY |
0.07 |
0.36 |
0.36 |
0.21 |
1.00 |
(a)
Using the marginal p.m.f.'s we get
![\begin{displaymath}
E[X] \; = \; 0*0.20 + 5*0.49 + 10*0.31
\; = \; 5.55 .\end{displaymath}](img51.gif)
![\begin{displaymath}
E[Y] \; = \;
0*0.07 + 5*0.36 + 10*0.36 + 15*0.21
\; = \; 8.55 .\end{displaymath}](img52.gif)
(b)
Let 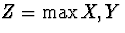 . Getting the p.m.f. of Z:
. Getting the p.m.f. of Z:
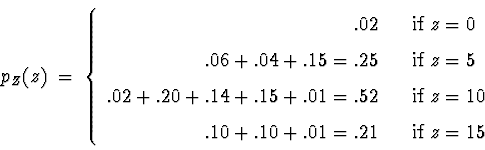
For example, looking at z=5, the event [Z=10] can be decomposed
into the mutually exclusive events
![$[X = 0 \, \& \, Y=5]$](img55.gif) or
or ![$[X = 5 \, \& \, Y=5]$](img56.gif) or
or
![$[X = 5 \, \& \, Y=0]$](img57.gif) . Note the pattern of the
values that are ``traced out'' in the table in this
event. Checking that the p.m.f. values sum to 1:
. Note the pattern of the
values that are ``traced out'' in the table in this
event. Checking that the p.m.f. values sum to 1:
.02 + .25 + .52 + .21 = 1 .
Thus,
![\begin{displaymath}
E[Z] \; = \; 0*.02 + 5*.25 + 10*.52 + 15*.21
\; = \; 9.6 .\end{displaymath}](img58.gif)


Next: Solution to Exercise 5.30.
Up: No Title
Previous: Solution to Exercise 5.06.
Dennis Cox
3/10/2001
![]()
![]()
![]() . Getting the p.m.f. of Z:
. Getting the p.m.f. of Z:
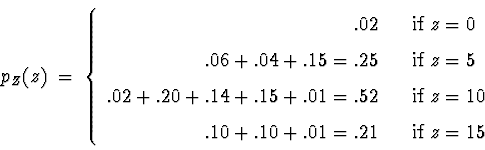
![]()