

Next: Solution to Exercise 5.54.
Up: No Title
Previous: No Title
(a)
Given information is:
![\begin{displaymath}
\mu \; = \; E[X_i] \; = \; 50 , \quad
\sigma^2 \; = \; V[X_i] \; = \; 1 , \quad \&
n \; = \; 100 .\end{displaymath}](img1.gif)
Therefore,
![\begin{displaymath}
E[\bar{X}] \; = \; \mu \; = \; 50 ,\end{displaymath}](img2.gif)
and
![\begin{displaymath}
V[\bar{X}] \; = \; \sigma^2/n \; = \; 1/100 ,\end{displaymath}](img3.gif)
so for the standard deviation (or standard error) of
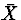 we have
we have
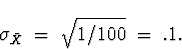
Letting Z denote a N(0,1) r.v. we have
by the CLT,
![\begin{displaymath}
P[ 49.75 < \bar{X} < 50.25 ] \; = \;
P \left[ \frac{49.75-5...
...ac{\bar{X}-\mu}{\sigma_{\bar{X}}}
< \frac{50.25-50}{.1} \right]\end{displaymath}](img6.gif)
![\begin{displaymath}
\; \doteq \;
P[ -2.5 < Z < 2.5 ] \; = \;
\Phi(2.5) - \Phi(-2.5) \; = \;
.9938 -.0062 \; = \; .9876 .\end{displaymath}](img7.gif)
(b)
Changing the above with
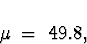
we have
![\begin{displaymath}
P[ 49.75 < \bar{X} < 50.25 ] \; = \;
P \left[ \frac{49.75-4...
...{\bar{X}-\mu}{\sigma_{\bar{X}}}
< \frac{50.25-49.8}{.1} \right]\end{displaymath}](img9.gif)
![\begin{displaymath}
\; \doteq \;
P[ -0.5 < Z < 4.5 ] \; = \;
\Phi(4.5) - \Phi(-0.5) \; = \;
1.000-.3085 \; = \; .6115 .\end{displaymath}](img10.gif)
Note that Table 3 stops tabulating 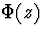 at
z = 3.49, and
at
z = 3.49, and 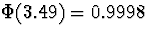 , so we can
safely take
, so we can
safely take 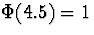 .
.
Dennis Cox
3/22/2001
![]()
![]()
![]()
![]()
![\begin{displaymath}
P[ 49.75 < \bar{X} < 50.25 ] \; = \;
P \left[ \frac{49.75-5...
...ac{\bar{X}-\mu}{\sigma_{\bar{X}}}
< \frac{50.25-50}{.1} \right]\end{displaymath}](img6.gif)
![]()
![]()
![\begin{displaymath}
P[ 49.75 < \bar{X} < 50.25 ] \; = \;
P \left[ \frac{49.75-4...
...{\bar{X}-\mu}{\sigma_{\bar{X}}}
< \frac{50.25-49.8}{.1} \right]\end{displaymath}](img9.gif)
![]()