

Next: Solution to Exercise 6.06.
Up: No Title
Previous: Solution to Exercise 5.48.
We are given
![\begin{displaymath}
\mu \; = \; E[X_i] \; = \; 2.65 , \quad
\sigma \; = \; \sqrt{V[X_i]} \; = \; .85 .\end{displaymath}](img14.gif)
Note that we are told that the Xi's are normally
distributed, so

is a N(0,1) r.v. for all sample sizes, i.e. no
appeal to the CLT is necessary.
(a)
Given that n = 25, we have that
![\begin{displaymath}
P[ \bar{X} \le 3.00 ] \; = \;
P \left[ \frac{\bar{X}-\mu}{\sigma/\sqrt{n}}
\le \frac{3.00-2.65}{.85/\sqrt{25}} \right]\end{displaymath}](img16.gif)
![\begin{displaymath}
\; = \; P[ Z \le 2.06 ] \; = \;
\Phi(2.06) \; = \; .9803\end{displaymath}](img17.gif)
For the second part, we have
![\begin{displaymath}
P[ 2.65 < \bar{X} \le 3.00 ]
\; = \;
P \left[ \frac{2.65-2...
...u}{\sigma/\sqrt{n}}
\le \frac{3.00-2.65}{.85/\sqrt{25}} \right]\end{displaymath}](img18.gif)
![\begin{displaymath}
\; = \; P[ 0 < Z \le 2.06 ] \; = \;
\Phi(2.06) - \Phi(0) \; = \;
.9803 - .5000 \; = \; .4803 .\end{displaymath}](img19.gif)
(b)
We want to find n so that
![\begin{displaymath}
P[ \bar{X} \le 3.00 ] \; = \; .99 .\end{displaymath}](img20.gif)
Now from Table 4.1 on p. 163 we have that
![\begin{displaymath}
P[Z \le 2.33] \; = \; .99 .\end{displaymath}](img21.gif)
Thus, we want
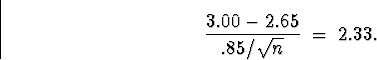
Algebraic manipulations give


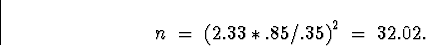
Of course, we can't take n = 32.02 since
n must be a whole number. Obviously, n = 32
will get us pretty close, but the problem says
``at least .99'' so we have to take n = 33
since n=32 is slightly too small.
Dennis Cox
3/22/2001
![]()

![\begin{displaymath}
P[ \bar{X} \le 3.00 ] \; = \;
P \left[ \frac{\bar{X}-\mu}{\sigma/\sqrt{n}}
\le \frac{3.00-2.65}{.85/\sqrt{25}} \right]\end{displaymath}](img16.gif)
![]()
![\begin{displaymath}
P[ 2.65 < \bar{X} \le 3.00 ]
\; = \;
P \left[ \frac{2.65-2...
...u}{\sigma/\sqrt{n}}
\le \frac{3.00-2.65}{.85/\sqrt{25}} \right]\end{displaymath}](img18.gif)
![]()
![]()
![]()
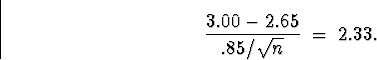


![]()