

Next: About this document ...
Up: No Title
Previous: Solution to Exercise 6.06.
Showing that 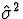 is and unbiased estimator of
is and unbiased estimator of
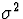 means showing that
means showing that 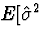 is
is
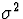 . Now we can split the fraction in the
definition of
. Now we can split the fraction in the
definition of 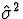 as in
as in
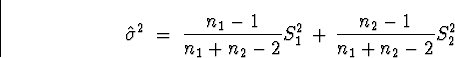
Using the linearity property of expectation and that
each Si2 is unbiased and unbiased estimator of 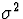 we have
we have
![\begin{displaymath}
E[ \hat{\sigma}^2 ] \; = \;
\frac{n_1 - 1}{n_1 + n_2 -2} E[S_1^2] \, + \,
\frac{n_2 - 1}{n_1 + n_2 -2} E[S_2^2]\end{displaymath}](img35.gif)
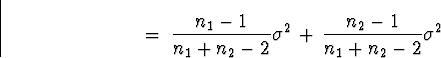
![\begin{displaymath}
\; = \;
\left[
\frac{n_1 - 1}{n_1 + n_2 -2} \, + \,
\frac{n_2 - 1}{n_1 + n_2 -2}
\right] \sigma^2\end{displaymath}](img37.gif)
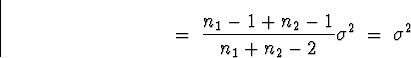
as desired.
Note:
One can see that any statistic of the form
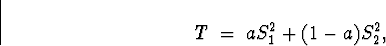
where a is a conastant will be an unbiased
estimator of 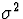 .
.
Dennis Cox
3/22/2001
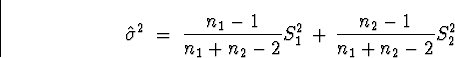
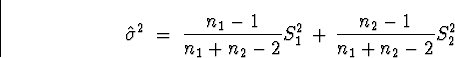
![\begin{displaymath}
E[ \hat{\sigma}^2 ] \; = \;
\frac{n_1 - 1}{n_1 + n_2 -2} E[S_1^2] \, + \,
\frac{n_2 - 1}{n_1 + n_2 -2} E[S_2^2]\end{displaymath}](img35.gif)
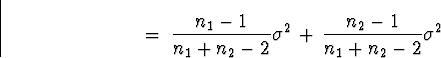
![\begin{displaymath}
\; = \;
\left[
\frac{n_1 - 1}{n_1 + n_2 -2} \, + \,
\frac{n_2 - 1}{n_1 + n_2 -2}
\right] \sigma^2\end{displaymath}](img37.gif)
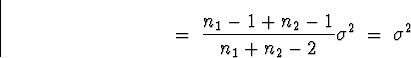
![]()