![\begin{displaymath}
E[X] \; = \; \int \, x f(x; \theta) \, dx
\; = \; \int_0^1 \, x (\theta +1) x^{\theta} \, dx\end{displaymath}](img2.gif)
![\begin{displaymath}
E[X] \; = \; \int \, x f(x; \theta) \, dx
\; = \; \int_0^1 \, x (\theta +1) x^{\theta} \, dx\end{displaymath}](img2.gif)
![\begin{displaymath}
\; = \; (\theta +1) \int_0^1 \, x^{\theta +1} \, dx
\; = \;...
...heta +2}
\right]_{x=0}^1
\; = \; \frac{\theta +1}{\theta +2} .\end{displaymath}](img3.gif)

![]()
![]()
![]()
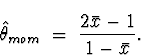
Putting the given data into minitab and computing the sample mean I get
![]()
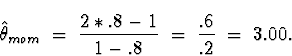
(b) The joint density is
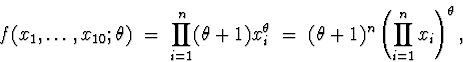
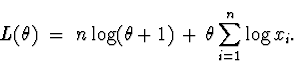
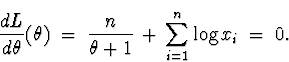
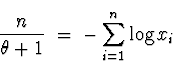
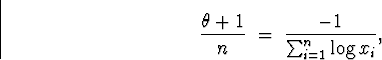
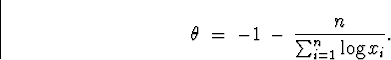

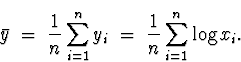
Back to minitab, I went to Calc ![]() Calculator and selected to
calculate ``Natural log'' (you have to find this in the list of functions) of
and entered C1 (where the original data is) and output to C2. The mean of
C2 is
Calculator and selected to
calculate ``Natural log'' (you have to find this in the list of functions) of
and entered C1 (where the original data is) and output to C2. The mean of
C2 is
![]()
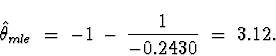
Note: The Maximum Likelihood Estimate and Method of Moments estimates agree pretty well. Which one should we use? To assess the accuracy of the different methods, let's perform a simulation experiment. Let's simulate values from the given distribution for a couple of parameter values near where we think the true parameter is - we'll just use our two different estimates. We'll compute the MOM (Method of Moments estimator) and MLE (Maximum Likelihood Estimator) for each sample, and repeat this, say, 100 times. Then we can see how accurate each estimator is by looking at bias, variance, and mean squared error. How can we simulate from this distribution? There is a general technique for simulating from distributions using the inverse c.d.f.: if U is a uniform r.v. on [0,1] and F is a c.d.f., then X = F-1 (U) is a r.v. whose distribution has the given c.d.f. F. This was already discussed in class and the proof is easy. The c.d.f. of X is defined to be
![]()
![]()
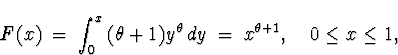
![]()
The results are shown in Table 1. We see that the standard errors of the two estimators are the same but the MOM has slightly less bias and RMSE (Root Mean Squared Error). In this example, the Method of Moments appears to be to be the better estimator.