.

  A random sample of size n = 64 is taken and the sample mean 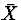$\bar{X}$ is computed. Assume the population mean is 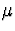$\mu$ = 120 and the population standard deviation is 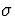$\sigma$ = 16.

(a) Find the mean and standard deviation of 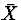$\bar{X}$.

Solution:

$$E[\bar{X}] \; = \; \mu \; = \; 120 .$$

$$V[\bar{X}] \; = \; \sigma^2/n \; = \; (16)^2/64 \; = \; 4 .$$

This gives the variance, and of course the standard deviation is the square root of this: 2.

(b) Find approximately $P[\bar{X} < 118]$. What major theorem are you using?

Solution:According to the Central Limit Theorem (CLT), 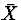$\bar{X}$ has approximately a Normal distribution with mean 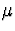$\mu$ and variance $\sigma^2/n$.

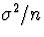$$P[\bar{X} < 118] \; = \; P \left[ \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} <\frac{118-120}{4} \right]$$

$$\; \approx \;P[Z < -.5] \; = \; 0.308538$$

where the table from Problem 2 was used to obtain the numerical answer.

A student discovered that I had made a mistake in this calculation: I used the variance instead of the standard deviation. I should have computed P[Z<-1] = 0.158655.
 

Problems? Questions? (I may have made a mistake, so don't hestitate to ask) dcox@stat.rice.edu
3/12/2001