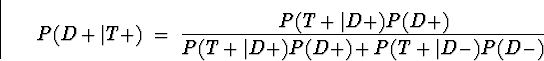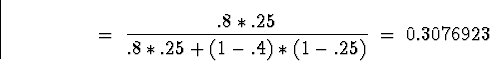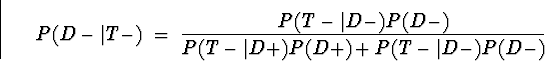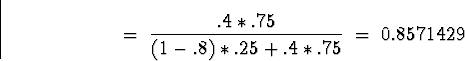

Next: About this document ...
Up: No Title
Previous: .
We define D+ as the event a randomly selected
person is positive for the disease of interest, and T+ the
event the person tests positive. The events D- and T- are
the corresponding complementary events of negative for disease
and testing negative, respectively.
Suppose that the prevalence is given by

Suppose that the sensitivity of the test is

and the specificity is
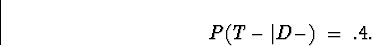
(a)
Compute the positive predictive power P(D+|T+).
Solution:
Using Bayes Theorem,
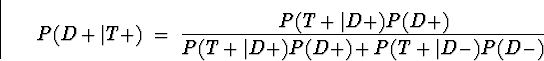
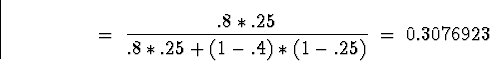
In spite of the great sensitivity (0.8), the test has a low
specificity (0.4), so the probability of disease after test
is only .308, compared with the probability of .25 before test
(the prevalence).
(b)
Compute the negative predictive power P(D-|T-).
Solution:
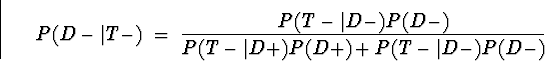
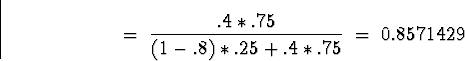
Note that the probability of no disease prior to test was .75,
so it has moved up to about .86 after a negative test, not a
dramatic improvement (because of the low specificity, again), but
still some improvement.
Problems? Questions? (I may have made a mistake, so don't
hestitate to ask)
dcox@stat.rice.edu
Dennis Cox
3/12/2001
![]()
![]()
![]()