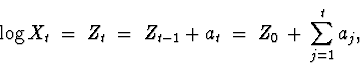
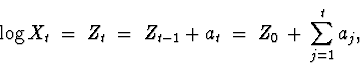 |
(1) |
The time series we will look at is the Dow-Jones index on 292 trading days ending 26 August 1994 which I got from an web site that seems to be defunct now (these things come and go so quickly).
In Section 2, we read these data into Splus and plot the series, logged series, differenced logged series, and the sample autocorrelation function. This provides reasonable evidence for the hypothesis.
In Section 3, we perform a little test of the geometric random walk model by constructing simulated data that would have the same distribution as the original data if the model is correct. We then present 20 plots: 19 are with simulated data and the 20th is of the real data. The real series is in a random place in the 20 plots. We challenge the reader to find the real series from among the plots.
In Section 4 we compute the periodogram (sample spectrum) and do a formal test for white noise based on the analysis of variance (ANOVA) of this sample spectrum. We also test for the presence of a day of week effect which would correspond to a period of 5 in the data.