(a) ![]() = .8,
= .8, ![]() = .55,
= .55, ![]() = for k > 2.
= for k > 2.
(a) ![]() = .8,
= .8, ![]() = .28,
= .28, ![]() = for k > 2.
= for k > 2.
Solution: In order for a given sequence to be a valid
autocorrelation function, we must of course have ![]() = 1. We assume this is intended, as the value of
= 1. We assume this is intended, as the value of ![]() is not explicitly stated. Furthermore, as in section 2.1.3, all of the
correlation matrices
is not explicitly stated. Furthermore, as in section 2.1.3, all of the
correlation matrices
![\begin{displaymath}\left[ \begin{array}{ccccc}1 & \rho_1 & \rho_2 & \ldots &... ...\ldots & 1\end{array} \right] \; = \; \mbox{\boldmath{P}}_n\end{displaymath}](img6.gif)
On p. 28 we see the conditions
Actually, all the < should be ![]() (because it is only necessary that the determinants that were evaluated
to produce these be nonnegative, not positive). In fact, these are necessary
but not sufficient for the given function to be a valid autocorrelation
function since they only verify positivity of the determinants of
(because it is only necessary that the determinants that were evaluated
to produce these be nonnegative, not positive). In fact, these are necessary
but not sufficient for the given function to be a valid autocorrelation
function since they only verify positivity of the determinants of ![]() for n = 1, 2, and 3, not all n. We can apply these conditions
to the given potential autocorrelation functions, and if any of the conditions
fails, then we know the given functions are not valid autocorrelation functions.
However, even if all three conditions are verified, then we cannot be sure
that the given function is an autocorrelation function because we don't
know about the sign of the determinant of
for n = 1, 2, and 3, not all n. We can apply these conditions
to the given potential autocorrelation functions, and if any of the conditions
fails, then we know the given functions are not valid autocorrelation functions.
However, even if all three conditions are verified, then we cannot be sure
that the given function is an autocorrelation function because we don't
know about the sign of the determinant of ![]() for n > 3.
for n > 3.
In both cases, clearly (1) and (2) hold, so there only remains to check (3). For the putative autocorrelation in (a),
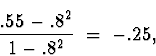
» format long » (.28-.8^2)/(1-.8^2) ans = -1.00000000000000It looks like it fails the condition as stated in the book, but doesn't fail it according to the amended statement as above (and mentioned in class).
So at this point, we don't really know more than when we started. It
is quite impossible to check the conditions that the determinant of ![]() is nonnegative for all n. However, as mentioned in class,
is nonnegative for all n. However, as mentioned in class, ![]() is a valid autocovariance if and only if
is a valid autocovariance if and only if
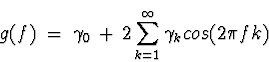 |
(1) |
Anyway, applying this fancier condition to the first alleged autocorrelation function, the corresponding spectrum (or spectral density function) is
Comments: I don't expect you to understand necessarily what is going on with this problem. The take home message is that it is nontrivial to determine if a given function is an autocorrelation function unless it is computed from a process known to be stationary.
Also, regarding the requirement of (strict) positive definiteness of
all ![]() vs. nonnegative definiteness, the latter is all that is needed, but if
one of the determinants is , that says there is some linear combination
of finitely many values of the process which is almost surely a constant
( if the process mean is ). This would mean that the process if perfectly
predictable given a large enough block of past observations. This never
occurs in practice, so the condition as stated in the text is ``safe''
in practice but not mathematically correct.
vs. nonnegative definiteness, the latter is all that is needed, but if
one of the determinants is , that says there is some linear combination
of finitely many values of the process which is almost surely a constant
( if the process mean is ). This would mean that the process if perfectly
predictable given a large enough block of past observations. This never
occurs in practice, so the condition as stated in the text is ``safe''
in practice but not mathematically correct.