Solution to Exercise 2.7  No Title  Solution to Exercise 2.5.

Solution to Exercise 2.6.

Problem Statement: ``Using the data of Exercise 2.1, calculate the periodogram for the periods 36, 18, 12, 9, 36/5, 6 and draw up an analysis of variance table showing the mean squares associated with these periods and the residual mean square.''

Solution: Don't you just love the Brits and the way that they cling to these archaic usages. Not. I guess I had enough people in my office about this one: just get the periodogram, test if the frequencies associated with the periods mentioned are significantly larger than for the other frequencies (these are the frequencies used for computing the ``residual mean square'').

There are 36 degrees of freedom in the data, but we lose 1 from the mean (DC component, if you are an ECE major), leaving 35. The problem axes us to test for significant size of frequencies 1/36, 1/18 = 2/36, 1/12 = 3/36, 1/9 = 4/36, 5/36, and 1/6 = 6/36, which just happen to be the first 6 (nonzero) Fourier frequencies (``fooyer freaks'', in street talk, where the subtleties of the French language are not appreciated). Basically, they want us to check for a low-frequency signal in these data. The 6 values of the periodogram have 12 degrees of freedom (2 each) and the and the other 12 ``residual'' values in the periodogram (corresponding to the higher frequencies) have 23 degrees of freedom. This can be seen in two ways: 23 = 35 - 12, the total degrees of freedom minus the degrees of freedom in the low frequencies being tested, and in the 12 ``residual''values, 11 have 2 degrees of freedom each and the last one has only 1 degree of freedom (this is always the case with an even sample size that the highest frequency only has a real or cosine part and hence only 1 degree of freedom), so $2 \times 11$ + 1 = 23.

Thus, our test statistic will be

$$F \; = \; \frac{ (\mbox{sum of first $6$\space periodogram v... ...2}{ (\mbox{sum of last $12$\space periodogram values})/6 } .$$ If the null hypothesis (that the values come from a Gaussian white noise) is true, then the sampling distribution of this test statistic has an F-distribution with (12,23) degrees of freedom. The null hypothesis is rejected if F is too large. The $5\%$ critical value in the upper tail of the F distribution with (12,23) degrees of freedom is 2.2036, so we reject the null hypothesis at the .05 level of significance if the observed value of the test statistic is larger than 2.2036. We can compute a p-value by computing the the area under the density of the F(12,23) distribution to the right of the observed value, and reject at the .05 level of significance if the p-value is less than .05 (reject at any level $\alpha$ if the p-value is less than $\alpha$).

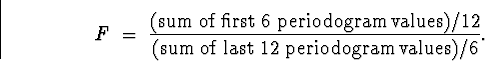
Here is the computation in Splus. I had already ``scanned'' in the data into reactor.

> spec=spec.pgram(reactor,taper=0,pad=0,detrend=F,demean=T)
> length(spec$spec)
[1] 19
> spec$freq[2]
[1] 0.02777778
> 1/36
[1] 0.02777778
> #No extra padding -- That's Good!!!
> pgram=10^(.1*spec$spec)
> plot(pgram)
> #Boy, that 3'rd frequency has a lot of energy
> test=(sum(pgram[2:7])/12)/(sum(pgram[8:19])/23)
> test
[1] 3.635956
> 1-pf(test,12,23)
[1] 0.003814983
> #OK, it's statistically significant.  There's something going
> #on in the 1st 6 fourier freq's.

The p-value is about 0.0038, which is pretty highly statistically significant. Yes, Virginia, there is a low frequency signal in these data.

Here's the corresponding calculation in Matlab, using the pdgrm function I created and using fcdf (the cumulative distribution function of the F-distribution) from the statistics toolbox (not available everywhere).

» pgram=pdgrm(z);
» test=(sum(pgram(1:6))/12)/(sum(pgram(7:18))/23);
» test

test =

    3.6360
» 1-fcdf(test,12,23)

ans =

    0.0038

Same p-value. The plot of the periodogram is shown here.

Axe me if you don't know what a p-value is.

3/10/1999