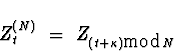Problem Statement: A circular stochastic process with period N is defined by Zt = Zt+N, for all t.
(a)
Show that when N = 2n, the latent roots of the ![]() autocorrelation matrix of Zt are
autocorrelation matrix of Zt are
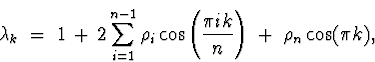 |
(3) |
(b)
Verify that as ![]() , with k/N fixed,
, with k/N fixed,
![]() tends to g(k/N)/2, where g(f) is the
spectral density function, showing that in the limit
the latent roots of the autocorrelation matrix trace
out the spectral curve.
tends to g(k/N)/2, where g(f) is the
spectral density function, showing that in the limit
the latent roots of the autocorrelation matrix trace
out the spectral curve.
Solution: This problem is probably the most difficult of the assignment. I contemplated not assigning it, but left it in in a foolish moment of confidence in the abilities of Rice students (not to detract from that). One problem was with the quaint British terminology of ``latent root'' and ``latent vector.'' We colonists know them more by their Anglicized (``Americanized(?)'') German terms of ``eigenvalues'' and ``eigenvectors.'' Then several students struggled with the sine-cosine stuff and I hinted ``complex exponential'' and they went away and never came back, probably because they eventually gave up. But then the real corker is figuring out how to get the correlation matrix written down correctly so that it incorporates the information that the process is circular. Since Zt = Zt+N = Zt-N, we have
| |
(4) |
So, when we get to ![]() in a row of the correlation
matrix, we start going backwards in the subscript.
in a row of the correlation
matrix, we start going backwards in the subscript.
The ![]() correlation matrix for
correlation matrix for
![]() is then
is then
![\begin{displaymath}
\mbox{\boldmath{R}} \; = \; \left[ \begin{array}
{cccccccccc...
...rho_{n-1} & \rho_{n-2} &
\cdots & \rho_1 & 1\end{array} \right]\end{displaymath}](img43.gif) |
(5) |
To complete the proof, we will show that
| |
(6) |
![]()
To prove (28), consider the first entry
of ![]() , i.e.
, i.e.
![]()
![]()
| |
(7) |
![]()
![]()
| |
(8) |
![]()
![]()
| |
(9) |
![]()
| |
(10) |
| |
(11) |
| |
(12) |
Now let's move on to the second component of
![]() . This is
. This is
![]()
![]()
| |
(13) |
![]()
![]()
| |
(14) |
![]()
| |
(15) |
| |
(16) |
You are probably getting the general idea by now. Can we make a formal mathematical argument? Let
![]()
![\begin{displaymath}
\mbox{\boldmath$M$} \; = \; \left[ \begin{array}
{cccccc}
0...
...ot & \cdot \\
0 & 0 & 0 & \cdots & 1 & 0
\end{array} \right]
\end{displaymath}](img82.gif)
![]()
The j'th entry of ![]() is
is
which is just the j'th entry of
![]() .
This shows that multiplying
.
This shows that multiplying ![]() times
times
![]() gives
gives ![]() back again but
multiplied by
back again but
multiplied by ![]() . We have
already worked out that
. We have
already worked out that ![]() , so
we have completed a fairly rigorous proof of (28).
, so
we have completed a fairly rigorous proof of (28).
Part (b) sort of seems trivial at this point. If
![]() but k/N = f is always fixed, then of course
but k/N = f is always fixed, then of course
where g(f) is given in (2.2.13), p. 40.
Clearly, we are assuming that
![]() as
as
![]() .
.
Well, this is all a little hard to swallow,
because the process was circular with period
N (remember that Zt = Zt+N for all
N which gave us that ![]() =
= ![]() for all k), so we can't be talking about the
same process for all N, i.e. there is a
different process for each N so all the
for all k), so we can't be talking about the
same process for all N, i.e. there is a
different process for each N so all the
![]() 's need an additional subscript or
something to show they depend on N, and
then they would be involved in taking the
limit as
's need an additional subscript or
something to show they depend on N, and
then they would be involved in taking the
limit as ![]() . Hmm.
What's it all about? Well, one can actually
make sense of what the authors are getting at
at this point. Let Zt be a fixed stationary process
satisfying a few nice properties (e.g., that
. Hmm.
What's it all about? Well, one can actually
make sense of what the authors are getting at
at this point. Let Zt be a fixed stationary process
satisfying a few nice properties (e.g., that
![]() ).
For each N construct a circular process of
period N from Zt by
).
For each N construct a circular process of
period N from Zt by