We will follow in part the proof of the Lindeberg CLT given in
class. We first derive the characteristic function of
a Bernoulli r.v. X with success probability 
:
Now let 
, 
be independent
Bernoulli random variables with success probability
, and put 
= 
.
The characteristic function of is
We wish to show that this converges to the
characteristic function of the Poisson
distribution with mean 
. Let us
derive what that characteristic function
is. If T is Poisson with mean ,
then
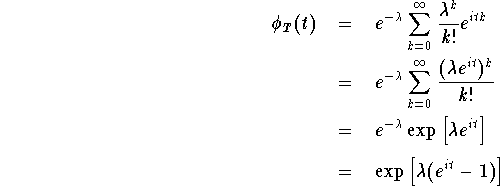
Thus, our goal is to show
Since 
= 
and exponentiation is a continuous function,
it follows that
Thus, it suffices to show
Now
Now we would like to apply the Lemma from class that was used in the proof of the Lindeberg CLT, namely:
See Lemma 1 in section 27 of Billingsley. Now
since it is the characteristic function of a Bernoulli r.v. (characteristic functions are always bounded by 1 in modulus). Similarly,
since it is the characteristic function of a Poisson
r.v. with mean . Thus, we obtain from
(10) and Lemma 1.1
without further difficulty that
Now with
we see that the summands in (14)
are simply the remainders in the first order
Taylor expansion of 
at 
.
It is not necessarily so easy to estimate
what this remainder is since 
is a
general complex number, i.e. has nonzero
real and imaginary parts. We know what the
remainder is like for Taylor series expansions
of a real variable, but not a general complex
variable.
However, let us assume for now that the remainder has the same order, that is
Thus, there exists an M such that 
and a 
such that
We wish to apply this result to
= 
.
We are given in condition (ii)
that 
0 as 
.
Since 
and
, condition (ii)
is the same as simply 
0. Thus,
So there exists 
such that for all 
,
and hence for all and all j, ,
Using this back in (14) we obtain
This proves (8), so to complete the problem we need to verify (16).
Now we turn to proving (16).
This is a well known result in complex
variables, but one can show it with a
real variable argument applied to the
real and imaginary parts. Denote
a complex number z by z = 
where 
and 
are both real. Now =
=
=
.
Further, we know
Since 
, of course
can be replaced with 
.
Thus,
Here, equation (29) follows by just
multiplying out the terms. Equation (30)
follows since 
= as
, and
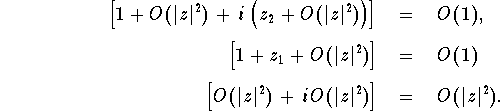
Also, in(30) we used that
, so 
.
