Solution to Problem 1.

1. [30 points] Let , , be independent discrete random variables with

 

Here, the , , is a sequence of positive constants and , , is a sequence of constants satisfying for all j.

Define

  

Assume

 

Show that .

Solution: We will use the following version of the Lindeberg C.L.T. (this is the one stated in class):

Let be a triangular array of random variables satisfying

(i)

as ;

(ii)

(Rowwise independence) For each n, the random variables , , , are mutually independent.

(iii)

(Centered) = 0 for all n and k.

(iv)

(Normalized) = 1.

(v)

(Lindeberg Condition) For every ,

Then

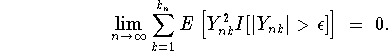
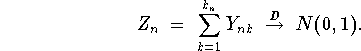
Now

 

so we don't need to do any centering. Also,

Therefore,

 

where is given in (3). Thus, if we define

then we claim the conditions of the Lindeberg CLT hold. We have so condition (i) holds. Condition (ii) is immediate since we are given that the 's are independent. Condition (iii) follows from (5). For condition (iv), observe that

by (6). Finally, to verify (v), let be given. Then

  

Of course, is 0 or , so if and only if . But by (4) there exists an such that for all ,

 

Hence, for all ,

 

and so for all ,

 

This proves the Lindeberg condition holds. Hence, we conclude

as required.