

Next: Solution to Exercise 4.10.
Up: No Title
Previous: Solution to Exercise 3.69.
Let X be the number in the sample of n = 1000 who carry the gene
for colon cancer. Assuming the sample is a random sample without
replacement (which is usually the understanding in these problems),
then X has in fact a hypergeometric distribution. However, we
aren't given the population size, so we couldn't compute with the
hypergeometric distribution. Furthermore, it is reasonable to assume
the population size is much larger than the sample size n = 1000,
so the binomial approximation to the hypergeometric applies, and
we can take 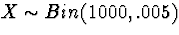 (note .005 = 1/200). Now,
we use the Poisson approximation to the Binomial as n is large and
p is small, so we can take
(note .005 = 1/200). Now,
we use the Poisson approximation to the Binomial as n is large and
p is small, so we can take 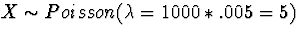 .
.(a)
![\begin{displaymath}
P[ 5 \le X \le 8 ] \; = \; P[ X \le 8 ] - P[ X \le 4 ]
\; = \; .932 - .440 \; = \; .492 .\end{displaymath}](img31.gif)
The numbers come from the table on p. 721.
(b)
![\begin{displaymath}
P[ X \ge 8 ] \; = \; 1 - P[ X \le 7 ] \; = \;
1 - .867 \; = \; .133 .\end{displaymath}](img32.gif)
Dennis Cox
2/19/2001
![]()
![]()