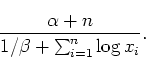Next: About this document ...
Up: Solutions to Final Exam
Previous: Solution to Problem 5.
Solution to Problem 6.
(6) [15 points]
The Pareto(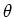 ) family of distributions has pdf given by
) family of distributions has pdf given by
where 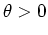 .
(a)
Verify that this is a legitimate pdf.
.
(a)
Verify that this is a legitimate pdf.
Solution:
Clearly
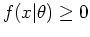 , so it is a legitimate pdf.
, so it is a legitimate pdf.
(b)
Is this an exponential family?
Solution:
which is an exponential family with
(c)
Does this distribution have a moment generating function
that is finite in a neighborhood of the origin?
Solution:
Note that
That is, the 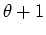 moment is not finite. If a
distribution has a mgf that is finite in a neighborhood of
moment is not finite. If a
distribution has a mgf that is finite in a neighborhood of 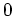 ,
then it has moments of all orders. Since this distribution does
not have moments of all orders, it cannot have a mgf that is
finite in a neighborhood of
,
then it has moments of all orders. Since this distribution does
not have moments of all orders, it cannot have a mgf that is
finite in a neighborhood of 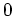 .
.
(d)
Suppose we have 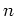 i.i.d. observations from the
Pareto(
i.i.d. observations from the
Pareto(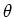 ) family with
) family with 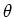 unknown.
Find the maximum likelihood estimator of
unknown.
Find the maximum likelihood estimator of 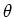 .
.
Solution:
The log likelihood is
except for the irrelevant terms involving the 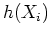 . Since
this is an exponential family, we can take derivatives and set to
. Since
this is an exponential family, we can take derivatives and set to
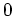 to find the mle (otherwise, we would have to check that it
gives a maximum):
to find the mle (otherwise, we would have to check that it
gives a maximum):
(d)
A Bayesian wants to make inferences about 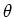 .
He uses a gamma(
.
He uses a gamma(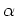 ,
,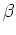 ) prior for
) prior for 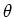 .
Show that the posterior for
.
Show that the posterior for 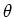 is also a
gamma distribution and find its parameters. Also,
find the posterior mean of
is also a
gamma distribution and find its parameters. Also,
find the posterior mean of 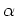 .
.
Solution:
The posterior is
This is a
pdf.
The posterior mean of 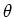 is
is



Next: About this document ...
Up: Solutions to Final Exam
Previous: Solution to Problem 5.
Dennis Cox
2003-01-18
![\begin{eqnarray*}
\int_1^{\infty} \; \theta x^{-(\theta+1)} \; dx
& \; = \; &
...
...]_{x=1}^{\infty} \\
& \; = \; & 0 - (-1) \\
& \; = \; & 1 .
\end{eqnarray*}](img148.png)
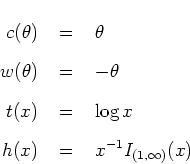
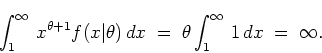
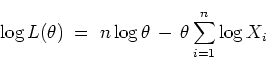
![\begin{displaymath}
n/\theta \, - \, \sum_{i=1}^n \log X_i
\; = \; 0 \; \Long...
...= \;
\left[ \frac{1}{n} \sum_{i=1}^n \log X_i \right]^{-1}.
\end{displaymath}](img157.png)
![\begin{displaymath}
f(\theta\vert x_1,\ldots,x_n) \; \propto \;
\theta^{\alpha-1+n} \exp[-\theta(1/\beta + \sum_{i=1}^n \log x_i) ] .
\end{displaymath}](img158.png)
![\begin{displaymath}
\mbox{gamma} \left(\alpha+n, \left[ 1/\beta + \sum_{i=1}^n \log x_i \right]^{-1} \right)
\end{displaymath}](img159.png)