


Next: Solution to Problem 6.
Up: Solutions to Final Exam
Previous: Solution to Problem 4.
Solution to Problem 5.
(5) [15 points]
Let 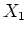 ,
, 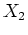 ,
,  be i.i.d.
be i.i.d.
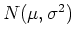 . Define
the sample mean and variance
. Define
the sample mean and variance
Assume 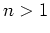 .
(a)
Show that
.
(a)
Show that ![$E[S_n^p]$](img121.png)
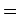
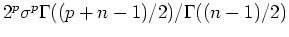 provided
provided 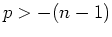 .
.
Solution:
We know that
Hence,
Now, if 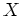
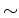 gamma(
gamma(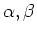 ) distribution, we have
) distribution, we have
We need 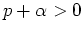 , i.e.
, i.e. 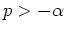 .
Hence,
.
Hence,
provided 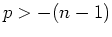 .
(b)
Find the UMVUE of
.
(b)
Find the UMVUE of 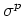 for
for 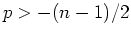 .
.
Solution:
We know that
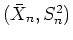 is complete and sufficient for
is complete and sufficient for
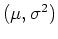 .
So we just need to find a function of
.
So we just need to find a function of 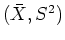 whose expectation is
whose expectation is
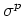 , and which has finite variance. From the result above, our answer is
, and which has finite variance. From the result above, our answer is
The restriction that 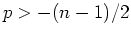 guarantees that this has
finite variance.
guarantees that this has
finite variance.
(c)
What is
![$E[\bar{X}_n/S_n ]$](img138.png) ? Find the UMVUE of
? Find the UMVUE of 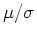 .
.
Solution:
We know that 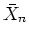 and
and 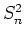 are independent, so
are independent, so
It follows that the UMVUE of
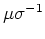 is
is
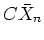 where
where



Next: Solution to Problem 6.
Up: Solutions to Final Exam
Previous: Solution to Problem 4.
Dennis Cox
2003-01-18
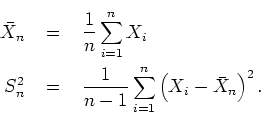
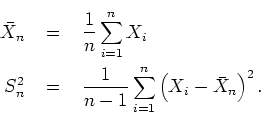
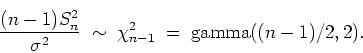
![\begin{eqnarray*}
E[X^p] & \; = \; & \int_0^{\infty} \,
\frac{1}{\Gamma(\alpha...
...
& \; = \; &
\frac{\Gamma(p+\alpha) \beta^p}{\Gamma(\alpha)} .
\end{eqnarray*}](img128.png)
![\begin{displaymath}
E[S_n^p] \; = \; E[(S_n^2)^{p/2}] \; = \;
\frac{\Gamma((p+n-1)/2) 2^{p/2} \sigma^p}{\Gamma((n-1)/2)(n-1)^{p/2}},
\end{displaymath}](img131.png)
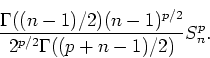
![\begin{eqnarray*}
E[\bar{X}_n/S_n] & \; = \; &
E[\bar{X}_n] E[ S_n^{-1} ] \\
...
...Gamma((n-2)/2) 2^{-1/2} \sigma^-1}{\Gamma((n-1)/2)(n-1)^{-1/2}}
\end{eqnarray*}](img142.png)