


Next: Solution to Problem 5.
Up: Solutions to Final Exam
Previous: Solution to Problem 3.
Solution to Problem 4.
(4) [20 points]
Let 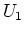 ,
, 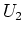 ,
, 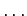 be i.i.d. uniform(0,1) rv's.
Define
be i.i.d. uniform(0,1) rv's.
Define
(a)
Show that
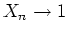 almost surely.
almost surely.
Solution:
Using the hint, let
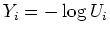 , then
it is easy to check that
, then
it is easy to check that 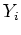 is exponential(1).
Hence,
is exponential(1).
Hence,
by the Strong Law of Large Numbers. Thus, taking
![$\exp[ - \cdot ]$](img110.png) of both sides, we see that
of both sides, we see that
(b)
Show that
Solution
By the Central Limit Theorem,
Apply the 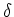 -method with
-method with
![$h(x) = \exp[- x]$](img115.png) ,
and noting that
,
and noting that
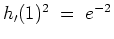 ,
we have
,
we have
Hint: logarithms.
Dennis Cox
2003-01-18
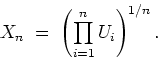
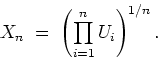
![\begin{displaymath}
- \log X_n \; = \; \frac{1}{n} \sum_{i=1}^n Y_i \;
\longrightarrow \; E[Y_i] = 1 , \quad \mbox{a.s.}
\end{displaymath}](img109.png)