


Next: Solution to Problem 4.
Up: Solutions to Final Exam
Previous: Solution to Problem 2.
Solution to Problem 3.
(3) [15 points]
Let 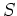 and
and 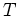 be statistics, and denote
the unknown parameter by
be statistics, and denote
the unknown parameter by 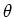 . Assume
the statistical model has either a pdf or
pmf for the observable. Let
. Assume
the statistical model has either a pdf or
pmf for the observable. Let 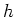 be any
reasonable (i.e., measurable) function.
For each of the following statements, either
give a proof or a counterexample.
(a)
If
be any
reasonable (i.e., measurable) function.
For each of the following statements, either
give a proof or a counterexample.
(a)
If 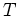 is sufficient for
is sufficient for 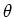 and
and 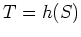 for
some function
for
some function 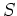 , then
, then 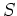 is sufficient for
is sufficient for 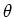 .
.
Solution:
Using the factorization theorem, we know for some
functions 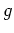 and
and 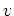
so by the factorization theorem, 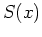 is sufficient.
The statement is True.
is sufficient.
The statement is True.
(b)
If 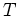 is complete for
is complete for 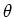 and
and 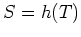 , then
, then
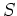 is complete.
is complete.
Solution:
Completeness of 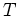 means for any function
means for any function 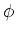 ,
,
![$E_{\theta} [ \phi(T) ] = 0$](img93.png) for all
for all 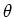 implies
implies
![$P_{\theta} [ \phi(T) = 0 ] = 1$](img94.png) for all
for all 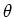 .
If
.
If 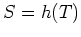 , then
, then 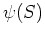
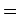
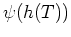
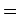
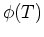 , so
, so
![$E_{\theta} [\psi(S)] = 0$](img98.png) for all
for all 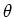 means
means
![$E_{\theta} [ \psi(h(T)) ] = 0$](img99.png) for all
for all 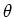 ,
which means
,
which means
![$P[ \psi(h(T)) = \psi(S) = 0 ] = 1$](img100.png) for all
for all 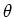 , so
, so 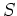 is complete. The statement
is True.
is complete. The statement
is True.
(c)
If 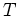 is ancillary for
is ancillary for 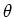 and
and 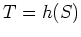 , then
, then
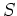 is ancillary.
is ancillary.
Solution:
Ancillarity means the distribution of 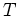 doesn't depend
on
doesn't depend
on 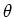 . Of course, if
. Of course, if 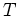 is a statistic and
is a statistic and 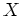 is
the data, then
is
the data, then 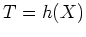 , but the distribution of
, but the distribution of 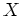 does depend on
does depend on 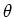 . Hence, the statement is
False.
. Hence, the statement is
False.



Next: Solution to Problem 4.
Up: Solutions to Final Exam
Previous: Solution to Problem 2.
Dennis Cox
2003-01-18