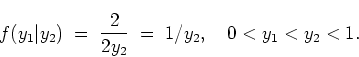Next: Solution to Problem 3.
Up: Solutions to Final Exam
Previous: Solution to Exercise 1.
Solution to Problem 2.
(2) [15 points]
Let 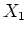 and
and 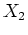 be i.i.d. uniform(0,1) rv's and
be i.i.d. uniform(0,1) rv's and
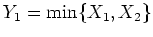 ,
,
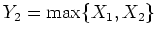 .
Show that the conditional distribution of
.
Show that the conditional distribution of  given
given
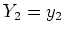 is uniform(0,
is uniform(0,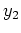 ).
).
Solution:
It is fairly easy to show that the joint pdf of 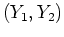 is
is
and the marginal pdf for 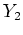 is
is
Thus, the conditional pdf for  given
given 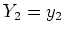 is
is
As a function of 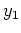 , we recognize this as the pdf for
the uniform(
, we recognize this as the pdf for
the uniform(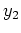 ) distribution.
) distribution.
Dennis Cox
2003-01-18