


Next: Solution to Problem 2.
Up: Solutions to Final Exam
Previous: Solutions to Final Exam
Solution to Exercise 1.
(1) [20 points]
Suppose 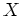 and
and 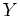 are independent random variables
with the distributions as given below. For each case,
determine the distribution of
are independent random variables
with the distributions as given below. For each case,
determine the distribution of 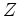
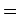
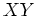 either by
giving the cdf, pdf, or pmf.
(a)
either by
giving the cdf, pdf, or pmf.
(a)
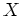 is uniform(0,1) and
is uniform(0,1) and 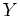 is exponential (
is exponential (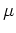 ).
).
Solution:
Since the joint distribution of 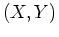 is continuous, we work
with the pdf
is continuous, we work
with the pdf
and apply the ``Jacobian'' theory. The transformation we will use is
The Jacobian is
Substituting in the joint pdf, we have
Note that
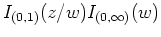 is
is 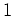 if and only if
if and only if
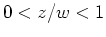

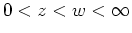 . For our
purposes, we note that
. For our
purposes, we note that
Now we want the marginal pdf 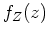 , which is
, which is
where
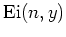
![$\int_1^{\infty} x^{-n} \exp[-yx] dx$](img50.png) is a
well known special function called the Exponential Integral.
(What? You don't know this special function? No problem.
I didn't count off as long as you got a correct integral
expression for
is a
well known special function called the Exponential Integral.
(What? You don't know this special function? No problem.
I didn't count off as long as you got a correct integral
expression for 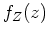 as in (1) or (2) below.)
An alternative expression (if you chose the transformation
as in (1) or (2) below.)
An alternative expression (if you chose the transformation
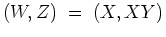 is
is
![\begin{displaymath}
f_Z (z) \; = \; \int_0^1 \, (\mu w)^{-1} \exp \left[ -z / (w \mu) \right] \, dw
I_{(0,\infty)} (z) .
\end{displaymath}](img52.png) |
(2) |
(b)
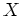 is uniform(0,1) and
is uniform(0,1) and 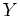 is Bernoulli(1/2).
is Bernoulli(1/2).
Solution:
Here, 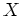 has a continuous distribution but
has a continuous distribution but 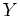 is discrete.
We can't use a Jacobian argument here. Also, we expect that
the distribution of
is discrete.
We can't use a Jacobian argument here. Also, we expect that
the distribution of 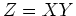 might be a mixture of discrete
and continuous, so we won't have a pdf or a pmf. It will be
necessary to give the distribution using the cdf.
Clearly,
might be a mixture of discrete
and continuous, so we won't have a pdf or a pmf. It will be
necessary to give the distribution using the cdf.
Clearly, 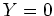 , which occurs with probability
, which occurs with probability 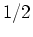 , means
, means
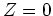 . If
. If 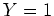 , then
, then 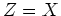 . Thus,
. Thus,
![$P[ Z = 0] = 1/2$](img59.png) ,
and if
,
and if 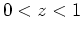 , then
, then
Putting it together, we have
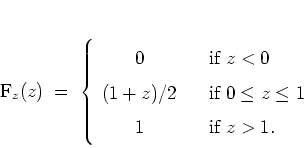 |
(4) |
(c)
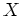 is Poisson(1) and
is Poisson(1) and 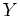 is Bernoulli(1/2).
is Bernoulli(1/2).
Solution:
Both 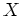 and
and 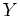 are discrete, so we don't use any Jacobians.
The distribution of
are discrete, so we don't use any Jacobians.
The distribution of 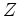 will be discrete with possible values
will be discrete with possible values
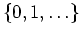 , the nonnegative integers. The pmf is
, the nonnegative integers. The pmf is



Next: Solution to Problem 2.
Up: Solutions to Final Exam
Previous: Solutions to Final Exam
Dennis Cox
2003-01-18
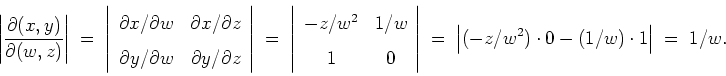
![\begin{eqnarray*}
f_{WZ} (w,z) & \; = \; & f_{XY} (z/w,w) \cdot (1/w) \\
& \;...
...{(0,1)} (z/w) \mu^{-1} w^{-1} \exp[-w/\mu] I_{(0,\infty)} (w) .
\end{eqnarray*}](img34.png)
![\begin{eqnarray*}
f_Z (z) & \; = \; & P[ Z = z ] \\
& \; = \; &
P[Z=z\vert Y...
...& & \mbox{if } z \in \{ 1 , 2 , \ldots \}.
\end{array} \right.
\end{eqnarray*}](img68.png)