We begin by stating the dominated convergence theorem. This may be found in any standard book that has measure theory - e.g. Chung's A Course in Probability Theory, or Royden's Real Analysis.
Now we state and prove the theorem of interest.
Proof. For convenience, let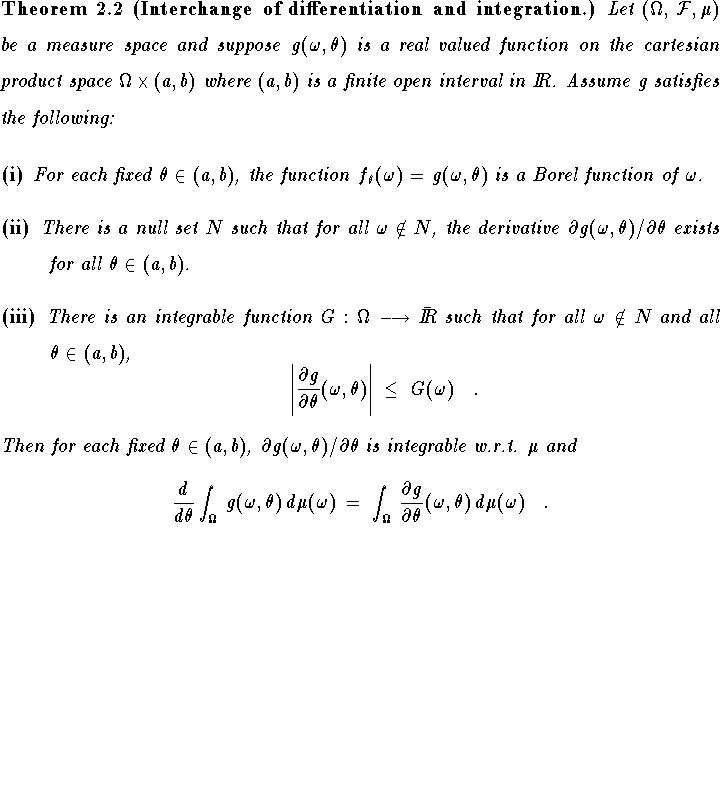 
=
.
Suppose 
, then by the mean
value theorem (Theorem 5.10, p. 108 of Rudin),
if 
and 
,
then
for some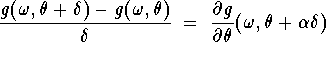 
, and in particular for all
,
Now let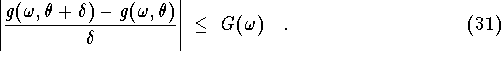 
be any sequence in 
converging to
0. Then by linearity of the integral,
Thus, we have for each fixed
, the sequence of functions
converges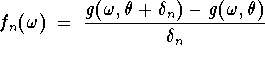 
-a.e. to
, and by (
),
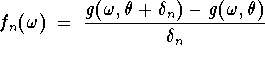, -a.e., and G is 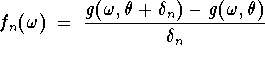-integrable by
assumption.
Hence, by the dominated convergence theorem (Theorem ),
,
i.e.
Since the sequence 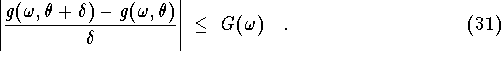0 was arbitrary,
it follows that
(See e.g. Theorem 4.2, p. 84 of Rudin for this result which
extends a limit from an arbitrary sequence to a continuous limit.)
This last display states that
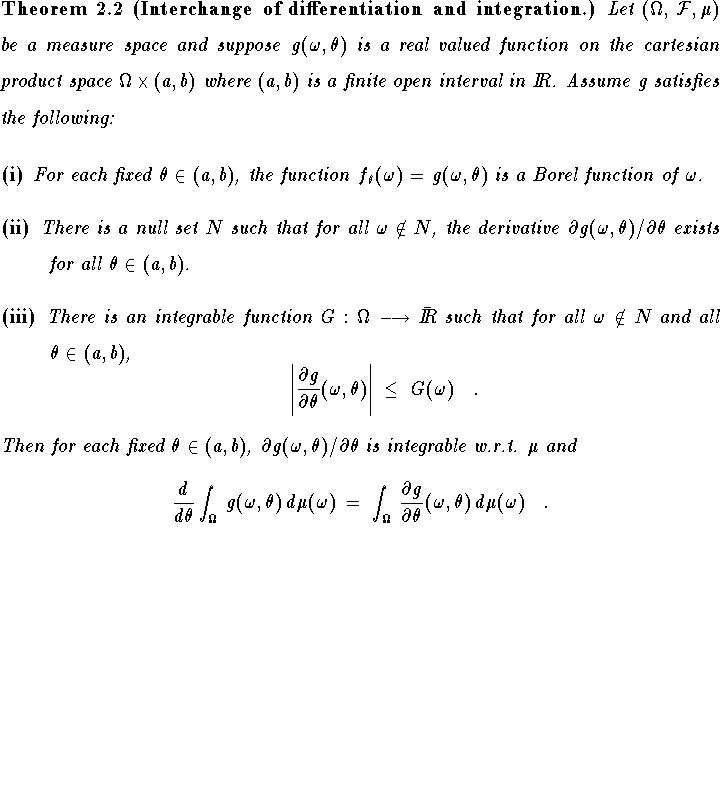is differentiable and the derivative is
the r.h.s. This proves the Theorem.
