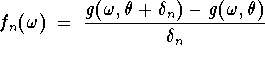 is
is
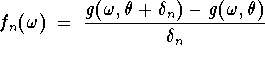 is Lebesgue measure and
is Lebesgue measure and 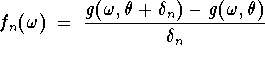 is counting measure and
is counting measure and
Let ![]() be a
parametric family of densities for a random observable
X, where X may be real valued, vector valued,
continuous, or discrete, or neither. (Of course,
if X is discrete you may prefer to think of
be a
parametric family of densities for a random observable
X, where X may be real valued, vector valued,
continuous, or discrete, or neither. (Of course,
if X is discrete you may prefer to think of
![]() as a probability mass function,
but we can just think of it as a density of
the discrete type or whatever.)
We assume the dominating measure
as a probability mass function,
but we can just think of it as a density of
the discrete type or whatever.)
We assume the dominating measure 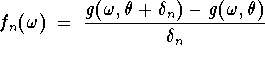 is
is
![]() -finite. (Don't worry about what
-finite. (Don't worry about what
![]() -finite means if you don't know.)
Basically, if X is continuous then
-finite means if you don't know.)
Basically, if X is continuous then
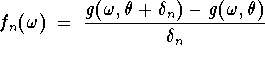 is Lebesgue measure and
is Lebesgue measure and ![]() =
dx below; if X is discrete then
=
dx below; if X is discrete then 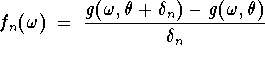 is counting measure and
is counting measure and ![]() =
= ![]() where the summation is over all
all possible values of x.) Thus, for instance
where the summation is over all
all possible values of x.) Thus, for instance
![]()
Now we have by the definition of a probability density that
Thus, differentiating both sides
Assuming we can interchange differentiation and integration,
Note that if f is strictly positive then
This identity will turn out to be useful for many purposes.
How can we justify the interchange of differentiation and
integration in (![]() )? Well, assume that the
parameter space is open and for each
)? Well, assume that the
parameter space is open and for each 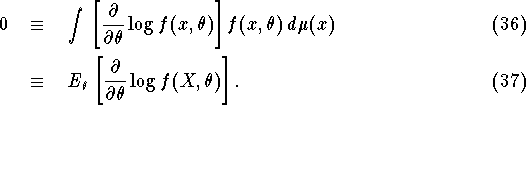 there is a
neighborhood
there is a
neighborhood ![]() and ``dominating'' function
and ``dominating'' function
![]() such that
such that
Then, assuming the usual measurability,
the conditions for Theorem ![]() will hold
with (a,b) of the theorem being the neighborhood
will hold
with (a,b) of the theorem being the neighborhood
![]() . As will be seen in the example
below, it is often easier to verify the identity
(
. As will be seen in the example
below, it is often easier to verify the identity
(![]() ) using ad hoc methods rather than
establishing (
) using ad hoc methods rather than
establishing (![]() ) and (
) and (![]() ).
).
The following result is very useful for many of the standard densities - those of so called ``exponential type.''
Proof. We will make use of the elementary inequality
Perhaps the easiest way to verify this is to
use the Taylor expansion ![]() =
=
![]() , valid for all
, valid for all
![]() . Then
. Then ![]() =
=
![]() and all
the summands are nonnegative when
and all
the summands are nonnegative when ![]() .
Suppose
.
Suppose ![]() is such that
is such that
![]() is contained in the neigborhood where
is contained in the neigborhood where ![]() is
finite. Then (
is
finite. Then (![]() ) gives us
) gives us
Similarly, by simple monotonicity properties of the exponential function,
The results in (![]() ), (
), (![]() ),
(
),
(![]() ), and (
), and (![]() ) can be combined into
) can be combined into
Since the sum of two nonnegative numbers is larger
than either of them, we can
combine (![]() ) and (
) and (![]() )
into the single inequality
)
into the single inequality
Let G(x) the the r.h.s. of (![]() ).
Since
).
Since ![]() is in the neighborhood
where
is in the neighborhood
where ![]() is finite,
is finite,
And
Therefore, 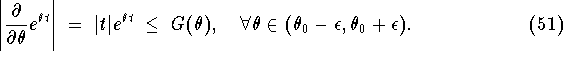 works as a dominating function
in Theorem
works as a dominating function
in Theorem ![]() and we have
and we have
![]()
which completes the proof.
![]()
This last result can be extended to the following.
Proof. Define the measure
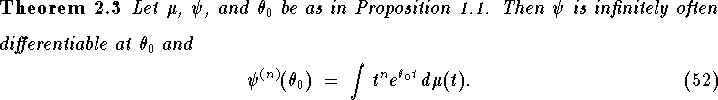
Now it follows from the proof of Proposition ![]() that
that
is finite in a neighborhood of 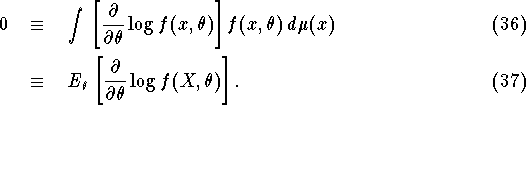 when n = 1.
Assuming
when n = 1.
Assuming  in a neighborhood
of
in a neighborhood
of 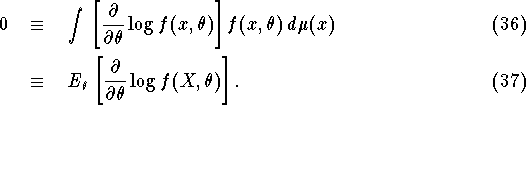 , it follows by the proof of Proposition
, it follows by the proof of Proposition
![]() that the same holds for
that the same holds for ![]() .
Thus, by induction, for each n,
.
Thus, by induction, for each n,  in a neighborhood of
in a neighborhood of 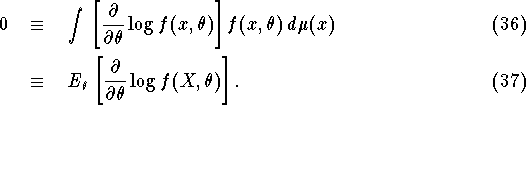 .
Hence, applying Proposition
.
Hence, applying Proposition ![]() , it follows
that
, it follows
that ![]() exists for each n
and may be computed by differentiating under the integral
sign. This completes the proof.
exists for each n
and may be computed by differentiating under the integral
sign. This completes the proof.
![]()
![]()